题目内容
【题目】以下茎叶图记录了甲，乙两组各四名同学单位时间内引体向上的次数，乙组记录中有一个数据模糊，无法确认，在图中以
表示.
（1）如果
，求乙组同学单位时间内引体向上次数的平均数和方差；
（2）如果
，分别从甲，乙两组中随机选取一名同学，求这两名同学单位时间内引体向上次数和为19的概率.
（注：方差
，其中
为
的平均数）.
【答案】（1）平均数
，方差
（2）
【解析】
（1）根据平均数和方差计算公式直接求得结果；（2）首先确定在甲、乙两组随机选取一名同学的所有情况，再找到次数和为
的情况，根据古典概型求得结果.
（1）当
时，由茎叶图可知，乙组同学的引体向上次数是
，，
，
平均数为：
方差为：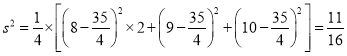
（2）记甲组四名同学分别为
，
，
，
，引体向上的次数依次为，，
，；
乙组四名同学分别为
，
，
，
，他们引体向上的次数依次为，，，
分别从甲、乙两组中随机选取一名同学，所有可能的结果有
个，即：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
用
表示“选出的两名同学的引体向上次数和为”这一事件
则中的结果有
个，它们是：，，，
故所求概率：
备战中考寒假系列答案
【题目】某超市随机选取
位顾客，记录了他们购买甲、乙、丙、丁四种商品的情况，整理成如下统计表，其中“√”表示购买，“×”表示未购买．
| 甲 | 乙 | 丙 | 丁 |
| √ | × | √ | √ |
| × | √ | × | √ |
| √ | √ | √ | × |
| √ | × | √ | × |
85 | √ | × | × | × |
| × | √ | × | × |
（Ⅰ）估计顾客同时购买乙和丙的概率；
（Ⅱ）估计顾客在甲、乙、丙、丁中同时购买
中商品的概率；
（Ⅲ）如果顾客购买了甲，则该顾客同时购买乙、丙、丁中那种商品的可能性最大？
【题目】为了巩固全国文明城市创建成果，今年吉安市开展了拆除违章搭建铁皮棚专项整治行为.为了了解市民对此项工作的“支持”与“反对”态度，随机从存在违章搭建的户主中抽取了男性、女性共
名进行调查，调查结果如下：
支持 | 反对 | 合计 | |
男性 |
|
|
|
女性 |
|
|
|
合计 |
|
|
|
（1）根据以上数据，判断是否有
的把握认为对此项工作的“支持”与“反对”态度与“性别”有关；
（2）现从参与调查的女户主中按此项工作的“支持”与“反对”态度用分层抽样的方法抽取
人，从抽取的人中再随机地抽取
人赠送小礼品，记这人中持“支持”态度的有
人，求的分布列与数学期望.
参考公式：
，其中
.
参考数据：
|
|
|
|
|
|
|
|
【题目】 某汽车租赁公司为了调查A, B两种车型的出租情况，现随机抽取这两种车型各50辆，分别统计了每辆车在某个星期内的出租天数，统计数据如下表:
A型车
出租天数 | 3 | 4 | 5 | 6 | 7 |
车辆数 | 3 | 30 | 5 | 7 | 5 |
B型车
出租天数 | 3 | 4 | 5 | 6 | 7 |
车辆数 | 10 | 10 | 15 | 10 | 5 |
(1)试根据上面的统计数据，判断这两种车型在本星期内出租天数的方差的大小关系(只需写出结果);
(2)现从出租天数为3天的汽车(仅限A, B两种车型)中随机抽取一辆，试估计这辆汽车是A型车的概率;
(3)如果两种车型每辆车每天出租获得的利润相同，该公司需要购买一辆汽车，请你根据所学的统计知识，给出建议应该购买哪一种车型，并说明你的理由．
