题目内容
如下图,已知M、N、P、Q分别是正方体ABCD—A1B
证明:延长DC到G,使DC=2CG.
连结GP,设GP与CC1交于点Q′,
则△CQ′G≌△C1Q′P.
∴CQ′=C1Q′.
∴Q′为CC1的中点.
∵Q是CC1的中点,
∴Q与Q′是同一个点.
∴P、Q、G三点共线.
同理,G、N、M三点共线.
∴直线PQ与直线MN相交于点G.
∴M、N、P、Q四点共面.
练习册系列答案
相关题目
（2012•蓝山县模拟）统计某校高三年级100名学生的数学月考成绩，得到样本频率分布直方图如下图所示，已知前4组的频数分别是等比数列{an}的前4项，后6组的频数分别是等差数列{bn}的前6项，
②
③
④
⑤
(本小题满分12分)
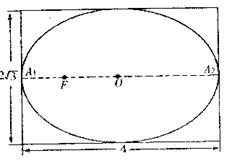
有一幅椭圆型彗星轨道图，长4cm，高
，如下图，
已知O为椭圆中心，A1，A2是长轴两端点，
|
（Ⅰ）建立适当的坐标系，写出椭圆方程，
并求出当彗星运行到太阳正上方时二者在图上的距离；
（Ⅱ）直线l垂直于A1A2的延长线于D点，|OD|=4，
设P是l上异于D点的任意一点，直线A1P，A2P分别
交椭圆于M、N（不同于A1，A2）两点，问点A2能否
在以MN为直径的圆上？试说明理由.
