题目内容
设x是实数,则“x>-1”是“|x|<1”的( )
分析:根据绝对值的定义,我们可以判断出“x>-1”⇒“|x|<1”为假命题,而“|x|<1”⇒“x>-1”为真命题,进而根据充要条件的定义,即可得到答案.
解答:解:当“x>-1”时,|x|>0,即“|x|<1”不一定成立,
故“x>-1”⇒“|x|<1”为假命题
即“x>-1”是“|x|<1”的不充分条件;
当“|x|<1”时,-1<x<1,“x>-1”成立,
故“|x|<1”⇒“x>-1”为真命题
即“x>-1”是“|x|<1”的必要条件;
故“x>-1”是“|x|<1”的必要不充分条件;
故选B
故“x>-1”⇒“|x|<1”为假命题
即“x>-1”是“|x|<1”的不充分条件;
当“|x|<1”时,-1<x<1,“x>-1”成立,
故“|x|<1”⇒“x>-1”为真命题
即“x>-1”是“|x|<1”的必要条件;
故“x>-1”是“|x|<1”的必要不充分条件;
故选B
点评:本题考查的知识点是充要条件,其中分别判断出“x>-1”⇒“|x|<1”与“|x|<1”⇒“x>-1”的真假,是解答本题的关键.

练习册系列答案
相关题目
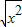
 ,g(x)=
,g(x)=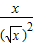
 ,g(x)=x-3
,g(x)=x-3