题目内容
设函数f（x）的定义域为A，且满足任意x∈A恒有f（x）+f（2-x）=2的函数是
- A.f（x）=log2x
- B.f（x）=2x
- C.
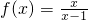
- D.f（x）=x2
C
分析：满足任意x∈A恒有f（x）+f（2-x）=2，则函数f（x）关于（1，1）中心对称，由此可得结论．
解答：∵满足任意x∈A恒有f（x）+f（2-x）=2
∴函数f（x）关于（1，1）中心对称
∵
=
的对称中心为（1，1）
故选C．
点评：本题考查函数的对称性，考查学生分析解决问题的能力，属于基础题．
分析：满足任意x∈A恒有f（x）+f（2-x）=2，则函数f（x）关于（1，1）中心对称，由此可得结论．
解答：∵满足任意x∈A恒有f（x）+f（2-x）=2
∴函数f（x）关于（1，1）中心对称
∵
=的对称中心为（1，1）故选C．
点评：本题考查函数的对称性，考查学生分析解决问题的能力，属于基础题．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
）与b=f（
）的大小关系为________．
）与b=f（
）的大小关系为 ．
）与b=f（
）的大小关系为（ ）．