题目内容
已知圆C:(x-3)2+(y-4)2=4,直线l1过定点A(1,0).
(1) 若l1与圆相切,求l1的方程;
(2) 若l1与圆相交于P、Q两点,线段PQ的中点为M,又l1与l2:x+2y+2=0的交点为N,判断AM·AN是否为定值?若是,则求出定值;若不是,请说明理由.
解:(1) ①若直线l1的斜率不存在,即直线是x=1,符合题意.
②若直线l1斜率存在,设直线l1为y=k(x-1),即kx-y-k=0.
 以下同解法1.
以下同解法1.

(解法3)用几何法
连结CA并延长交l2于点B,kAC=2,kl2=- ,
,
∴CB⊥l2.如图所示,△AMC∽△ABN,则
可得AM·AN=AC·AB=2 ·
· =6,是定值.
=6,是定值.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 ”是“
”是“ ”的( )
”的( )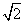 =0上点P作圆x2+y2=1的两条切线,若两条切线的夹角是60°,则点P的坐标是__________.
=0上点P作圆x2+y2=1的两条切线,若两条切线的夹角是60°,则点P的坐标是__________. ;
; .
. 终边上一点
终边上一点 ,求
,求 的值.
的值.