题目内容
函数f（x）=|logax|（0＜a＜1）的单调递减区间是（ ）
分析：本题是含有绝对值的对数型函数的单调性的问题，函数f（x）=|logax|（0＜a＜1）的图象由函数y=logax图象的翻折变化可得，结合对数函数的性质与绝对值的意义，直接得出其单调区间．
解答：
解：函数f（x）=|logax|（0＜a＜1）的图象由函数y=logax图象的翻折变化可得，如图．
知f（x）=|logax|（0＜a＜1）图象是由f（x）=logax（0＜a＜1）的图象中x轴下方的图象对称地翻到了x轴的上方而得到，
根据f（x）=logax（0＜a＜1）性质知，
f（x）=|logax|（0＜a＜1）在区间（0，1]上是减函数．
故选C．
解：函数f（x）=|logax|（0＜a＜1）的图象由函数y=logax图象的翻折变化可得，如图．知f（x）=|logax|（0＜a＜1）图象是由f（x）=logax（0＜a＜1）的图象中x轴下方的图象对称地翻到了x轴的上方而得到，
根据f（x）=logax（0＜a＜1）性质知，
f（x）=|logax|（0＜a＜1）在区间（0，1]上是减函数．
故选C．
点评：本题是含有绝对值的对数型函数的单调性的问题，含有绝对值的函数图象，其特点是x轴上方的不变化，下方的图象翻到了上方，同时单调性也增减对换．
练习册系列答案
阅读快车系列答案
相关题目
的定义域为M，g(x)＝lo
(2＋x＝6x2)的单调递减区间是开区间N，设全集U＝R，则M∩CU(N)＝________．
）2+7lo
+3≤0的解集为M，求当x∈M时，函数f（x）=（lo
）（lo
）的最大值和最小值．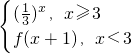
，则f（2+lo
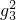）的值为________．