题目内容
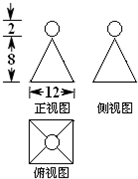 一几何体的三视图如图所示,正视图与侧视图是全等图形,则这个几何体的表面积是( )
一几何体的三视图如图所示,正视图与侧视图是全等图形,则这个几何体的表面积是( )分析:由几何体的三视图知,这个几何体的下部是底面边长为12高为8的正四棱锥,上部是直径为2的球,由此能求出这个几何体的表面积.
解答:解:由几何体的三视图知,这个几何体的下部是底面边长为12高为8的正四棱锥,
上部是直径为2的球,
∵正四棱锥的底面边长为12,高为8,
∴正四棱的侧面的等腰三角形的高为
=10,
∴这个几何体的表面积S=122+4×(
×12×10)+4π×(
)2=384+4π.
故选A.
上部是直径为2的球,
∵正四棱锥的底面边长为12,高为8,
∴正四棱的侧面的等腰三角形的高为
(
|
∴这个几何体的表面积S=122+4×(
| 1 |
| 2 |
| 2 |
| 2 |
故选A.
点评:本题考查由几何体的三视图求几何体的表面积,是基础题.解题时要认真审题,注意空间思维能力和空间想象能力的培养.

练习册系列答案
相关题目
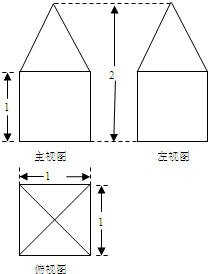
一几何体的三视图如图所示,则该几何体的体积是( )

| A、2 | ||||
B、
| ||||
C、1+
| ||||
D、1+
|
 已知一几何体的三视图如图,正视图和侧视图都是矩形,俯视图为正方形,在该几何体上任意选择5个顶点,它们可能是如下各种几何形体的5个顶点,这些几何形体是(写出所有正确结论的编号)
已知一几何体的三视图如图,正视图和侧视图都是矩形,俯视图为正方形,在该几何体上任意选择5个顶点,它们可能是如下各种几何形体的5个顶点,这些几何形体是(写出所有正确结论的编号) 已知一几何体的三视图如图所示,则其体积为
已知一几何体的三视图如图所示,则其体积为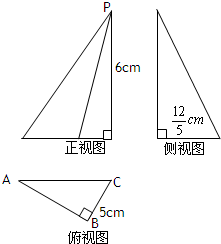 一几何体的三视图如图:
一几何体的三视图如图: (2011•开封一模)已知一几何体的三视图如图,则该几何体外接球的表面积为
(2011•开封一模)已知一几何体的三视图如图,则该几何体外接球的表面积为