题目内容
给出下列结论,其中正确的是
- A.渐近线方程为
 的双曲线的标准方程一定是
的双曲线的标准方程一定是
- B.抛物线
 的准线方程是
的准线方程是
- C.等轴双曲线的离心率是

- D.椭圆
 的焦点坐标是
的焦点坐标是 ,
,
C
分析:A:根据双曲线的性质可得:以 为渐近线方的双曲线标准方程为:
为渐近线方的双曲线标准方程为: .
.
B:根据抛物线的性质可得此抛物线的准线方程为:y= .
.
C:由等轴双曲线的定义可得:a=b,进而得到其离心率e= .
.
D:由题意可得m与n的大小不确定,所以不能判断椭圆的焦点位置.
解答:A:根据双曲线的性质可得:以 为渐近线方的双曲线标准方程为:
为渐近线方的双曲线标准方程为: ,所以A错误.
,所以A错误.
B:抛物线 的标准方程为:x2=-2y,所以根据抛物线的性质可得此抛物线的准线方程为:y=
的标准方程为:x2=-2y,所以根据抛物线的性质可得此抛物线的准线方程为:y= ,所以B错误.
,所以B错误.
C:由等轴双曲线的定义可得:a=b,所以c= a,所以等轴双曲线的离心率e=
a,所以等轴双曲线的离心率e= ,所以C正确.
,所以C正确.
D:因为椭圆的标准方程为: ,并且m与n的大小不确定,所以不能判断椭圆的焦点位置,所以D错误.
,并且m与n的大小不确定,所以不能判断椭圆的焦点位置,所以D错误.
故选C.
点评:解决此类问题的关键是熟练掌握椭圆、双曲线、抛物线的方程与有关性质,此题考查学生的基础知识与学生的运算能力.
分析:A:根据双曲线的性质可得:以
 为渐近线方的双曲线标准方程为:
为渐近线方的双曲线标准方程为: .
.B:根据抛物线的性质可得此抛物线的准线方程为:y=
 .
.C:由等轴双曲线的定义可得:a=b,进而得到其离心率e=
 .
.D:由题意可得m与n的大小不确定,所以不能判断椭圆的焦点位置.
解答:A:根据双曲线的性质可得:以
 为渐近线方的双曲线标准方程为:
为渐近线方的双曲线标准方程为: ,所以A错误.
,所以A错误.B:抛物线
 的标准方程为:x2=-2y,所以根据抛物线的性质可得此抛物线的准线方程为:y=
的标准方程为:x2=-2y,所以根据抛物线的性质可得此抛物线的准线方程为:y= ,所以B错误.
,所以B错误.C:由等轴双曲线的定义可得:a=b,所以c=
 a,所以等轴双曲线的离心率e=
a,所以等轴双曲线的离心率e= ,所以C正确.
,所以C正确.D:因为椭圆的标准方程为:
 ,并且m与n的大小不确定,所以不能判断椭圆的焦点位置,所以D错误.
,并且m与n的大小不确定,所以不能判断椭圆的焦点位置,所以D错误.故选C.
点评:解决此类问题的关键是熟练掌握椭圆、双曲线、抛物线的方程与有关性质,此题考查学生的基础知识与学生的运算能力.

练习册系列答案
相关题目
 )|的最小正周期是
)|的最小正周期是 ;
;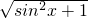 )有无奇偶性不能确定.
)有无奇偶性不能确定.