Question

正方形ABCD的边长是2,E、F分别是AB和CD的中点,将正方形沿EF折成直二面角(如图).M为矩形AEFD内一点,如果∠MB′E=∠MB′C′,MB′和平面B′C′F所成角的正切值为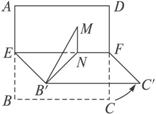,那么点M到直线EF的距离为__________.

Answer 1

答案:

解析:如图,过点M作MN⊥EF于N.由已知得MN⊥面EB′C′F.

∴∠MB′N为直线MB′与平面B′C′F所成的角,即tan∠MB′N=.

又因∠MB′E=∠MB′C′.

易知B′N为∠EB′C′的平分线.

∴B′N=2B′E=.

∴MN=B′N·tan∠MB′N=.