题目内容
在直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为 .曲线
.曲线 的参数方程为
的参数方程为 ,则直线
,则直线 和曲线
和曲线 的公共点有( )
的公共点有( )
A. 个 个 | B.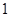 个 个 | C.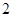 个 个 | D.无数个 |
B
解析试题分析: 即y=x+4,
即y=x+4,
即 ,
,
因为, ,所以,直线与圆相切,直线
,所以,直线与圆相切,直线 和曲线
和曲线 的公共点有1个,选B。
的公共点有1个,选B。
考点:本题主要考查参数方程与普通方程的互化,直线与圆的位置关系。
点评:小综合题,将参数方程化为普通方程,实现了“化生为熟”,研究直线与圆的位置关系,两种思路,一是“代数法”,二是“几何法”。

练习册系列答案
相关题目
在极坐标系中,以极点为坐标原点,极轴为x轴正半轴,建立直角坐标系,点M(2, )的直角坐标是( )
)的直角坐标是( )
| A.(2,1) | B.( ,1) ,1) | C.(1, ) ) | D.(1,2) |
在极坐标系中,点A(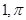 )到直线
)到直线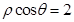 的距离是( ).
的距离是( ).
| A.1 | B.2 | C.3 | D.4 |
在极坐标系中,与点 关于极点对称的点的坐标是 ( )
关于极点对称的点的坐标是 ( )
A. | B. | C. | D. |
极坐标方程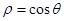 和参数方程
和参数方程 (
( 为参数)所表示的图形分别是
为参数)所表示的图形分别是
| A.圆、直线 | B.直线、圆 | C.圆、圆 | D.直线、直线 |
极坐标系中,以(9, )为圆心,9为半径的圆的极坐标方程为( )
)为圆心,9为半径的圆的极坐标方程为( )
A. | B. |
C. | D. |
在极坐标系中,曲线 关于( )对称。
关于( )对称。
A.直线 | B.直线 | C.点 | D.极点 |
 的极坐标方程是
的极坐标方程是 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴的正半轴建立平面直角坐标系,则曲线
轴的正半轴建立平面直角坐标系,则曲线 与直线
与直线 的两个交点之间的距离为 .
的两个交点之间的距离为 .