题目内容
设虚数z=(x-2)+yi,(x,y∈R),又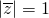 ,那么
,那么 的取值范围是
的取值范围是
- A.
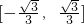
- B.
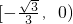 ∪
∪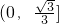
- C.

- D.
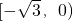 ∪
∪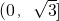
A
分析:根据z=(x-2)+yi,(x,y∈R),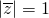 ,可知方程表示以(2,0)为圆心,1为半径的圆,利用参数法,构建函数,进而利用导数求出
,可知方程表示以(2,0)为圆心,1为半径的圆,利用参数法,构建函数,进而利用导数求出 的取值范围.
的取值范围.
解答:由题意,∵z=(x-2)+yi,(x,y∈R),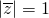
∴(x-2)2+y2=1
设x=2+cosα,y=sinα,α∈[0,2π]
∴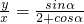
设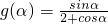 ,∴
,∴ =
=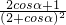
令g′(α)=0,∴2cosα+1=0
∵α∈[0,2π],∴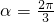 或
或
∵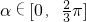 上,g′(α)>0,
上,g′(α)>0,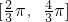 上,g′(α)<0,
上,g′(α)<0,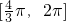 上,g′(α)>0
上,g′(α)>0
∴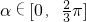 上单调增,
上单调增,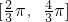 上单调减,
上单调减,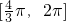 上单调增
上单调增
∴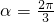 时,函数取得最大值为:
时,函数取得最大值为: ;
; 时,函数取得最小值为-
时,函数取得最小值为-
故选A.
点评:本题以虚数的模为载体,考查圆的方程的运用,考查利用导数求最值,有一定的综合性.
分析:根据z=(x-2)+yi,(x,y∈R),
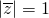 ,可知方程表示以(2,0)为圆心,1为半径的圆,利用参数法,构建函数,进而利用导数求出
,可知方程表示以(2,0)为圆心,1为半径的圆,利用参数法,构建函数,进而利用导数求出 的取值范围.
的取值范围.解答:由题意,∵z=(x-2)+yi,(x,y∈R),
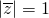
∴(x-2)2+y2=1
设x=2+cosα,y=sinα,α∈[0,2π]
∴
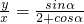
设
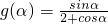 ,∴
,∴ =
=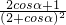
令g′(α)=0,∴2cosα+1=0
∵α∈[0,2π],∴
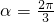 或
或
∵
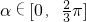 上,g′(α)>0,
上,g′(α)>0,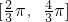 上,g′(α)<0,
上,g′(α)<0,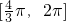 上,g′(α)>0
上,g′(α)>0∴
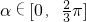 上单调增,
上单调增,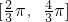 上单调减,
上单调减,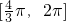 上单调增
上单调增∴
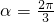 时,函数取得最大值为:
时,函数取得最大值为: ;
; 时,函数取得最小值为-
时,函数取得最小值为-
故选A.
点评:本题以虚数的模为载体,考查圆的方程的运用,考查利用导数求最值,有一定的综合性.

练习册系列答案
相关题目