题目内容
(本题满分12分)已知定义域为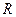 的函数
的函数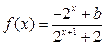 是奇函数.
是奇函数.
(1)求 的值
的值
(2)判断函数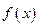 的单调性
的单调性
(3)若对任意的 ,不等式
,不等式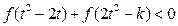 恒成立,求
恒成立,求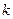
 的取值范围
的取值范围
解:(1)因为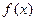 在定义域为
在定义域为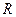 上是奇函数,所以
上是奇函数,所以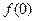 =0,即
=0,即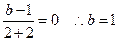 …….....3分
…….....3分
(2)由(Ⅰ)知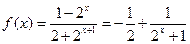 ,
,
设
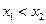 则
则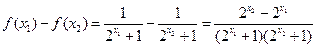
因为函数y=2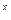 在R上是增函数且
在R上是增函数且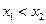 ∴
∴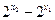 >0
>0
又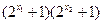 >0 ∴
>0 ∴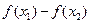 >0即
>0即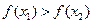
∴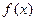 在
在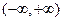 上为减函数. ………………………………....………...…..7分
上为减函数. ………………………………....………...…..7分
(3)因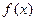 是奇函数,从而不等式:
是奇函数,从而不等式: 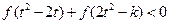
等价于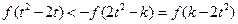 ,……………….……………………...….8分
,……………….……………………...….8分
因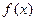 为减函数,由上式推得:
为减函数,由上式推得: .
.
即对一切 有:
有: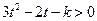 , ………..………………………….………....10分
, ………..………………………….………....10分
从而 判别式
判别式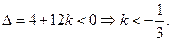 ………..…..……………………………..……...12分
………..…..……………………………..……...12分
解析

练习册系列答案
相关题目
 的定义域为
的定义域为 ,对于任意正实数
,对于任意正实数 恒有
恒有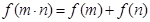 ,且当
,且当 时,
时,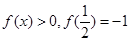
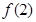 的值;
的值; 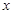 的不等式
的不等式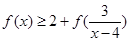 .
.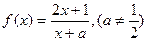 ,
, ,证明
,证明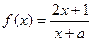 在区间
在区间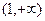 上是增函数;
上是增函数;
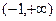 上是单调函数,试求实数
上是单调函数,试求实数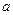 的取值范围。
的取值范围。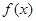 的最小值为1,且
的最小值为1,且 .
.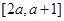 上不单调,求实数
上不单调,求实数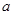 的取值范围;
的取值范围;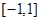 上,
上,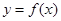 的图象恒在
的图象恒在 的图象上方,试确定实数
的图象上方,试确定实数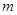 的
的 取值范围。
取值范围。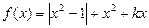 ,且定义域为(0,2).
,且定义域为(0,2).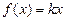 +3在(0,2)上的解;
+3在(0,2)上的解;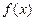 是定义域(0,2)上的单调函数,求实数
是定义域(0,2)上的单调函数,求实数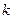 的取值范围;
的取值范围;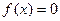 在(0,2)上有两个不同的解
在(0,2)上有两个不同的解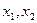 ,求k的取值范围。
,求k的取值范围。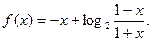
 的值;
的值; 在定义域内的单调性并给予证明.
在定义域内的单调性并给予证明. |x|在x∈[-1,1]的图象上有两点A、B,
|x|在x∈[-1,1]的图象上有两点A、B, AB∥
AB∥