题目内容
已知点A（1，1，0），对于z轴正半轴上任意一点P，在y轴上是否存在一点B，使得PA⊥AB恒成立？若存在，求出B点的坐标，若不存在，说明理由．
分析：在y轴上是否存在一点B，使得PA⊥AB恒成立，一般都假设存在，然后利用数列积为0建立等式，解之即可求出所求．
解答：解：设P（0，0，z），z＞0，假设在y轴上是否存在一点B（0，y，0）使得PA⊥AB恒成立
则
•
=0
而
=（1，1，-z），
=（-1，y-1，0）
∴
•
=1×（-1）+1×（y-1）+（-z）×0=y-2=0
解得y=2
∴存在点B为（0，2，0）时，PA⊥AB恒成立
则
| PA |
| AB |
而
| PA |
| AB |
∴
| PA |
| AB |
解得y=2
∴存在点B为（0，2，0）时，PA⊥AB恒成立
点评：本题主要考查了利用空间向量数量积判断垂直关系，同时考查了运算求解的能力，属于容易题．
练习册系列答案
阅读快车系列答案
相关题目
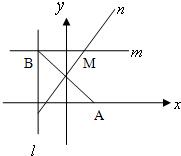已知点A（1，0），定直线l：x=-1，B为l上的一个动点，过B作直线m⊥l，连接AB，作线段AB的垂直平分线n，交直线m于点M．
，点A的坐标为(1＋
，
)，
＝m·
(m为常数)，
·
＝|
的比分别为λ1、λ2，求λ1＋λ2的值．