题目内容
矩形ABCD中,AB=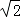 ,BC=2,Q为AD的中点,将△ABQ、△CDQ沿BQ、CQ折起,使得AQ、DQ重合,记A、D重合的点为P.
,BC=2,Q为AD的中点,将△ABQ、△CDQ沿BQ、CQ折起,使得AQ、DQ重合,记A、D重合的点为P.
(1)求二面角B﹣PQ﹣C的大小;
(2)证明PQ⊥BC;
(3)求直线PQ与平面BCQ所成的角的大小.
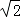 ,BC=2,Q为AD的中点,将△ABQ、△CDQ沿BQ、CQ折起,使得AQ、DQ重合,记A、D重合的点为P.
,BC=2,Q为AD的中点,将△ABQ、△CDQ沿BQ、CQ折起,使得AQ、DQ重合,记A、D重合的点为P.(1)求二面角B﹣PQ﹣C的大小;
(2)证明PQ⊥BC;
(3)求直线PQ与平面BCQ所成的角的大小.
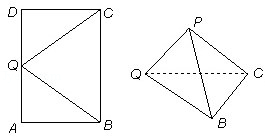
(1)解:在矩形ABCD中,AB⊥AQ,DC⊥DQ,
所以,在折起后,有PB⊥PQ,APC⊥PQ,
所以∠BPC就是所求的二面角的平面角.
因为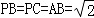 ,BC=2,
,BC=2,
所以PB2+PC2=BC2,
即△PBC是直角三角形,所以∠BPC=90°.
(2)证明:由已知可得△BCQ、△BCP都是等腰三角形,取BC中点M,连PM、QM,
则有PM⊥BC,QM⊥BC,
因为PM∩QM=M,PM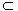 平面PQM,QM
平面PQM,QM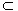 平面PQM,
平面PQM,
所以BC⊥平面PQM,
因为PQ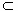 平面PQM,
平面PQM,
所以PQ⊥BC.
(3)解:由(2)知BC⊥平面PQM,而BC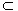 平面BCQ,
平面BCQ,
所以平面PQM⊥平面BCQ.
又平面PQM∩平面BCQ=QM,
所以,作PN⊥QM,
有PN⊥平面BCQ,
所以QN是PQ在平面BCQ内的射影,
所以∠PQN就是所求的角.
在等腰△BCQ中,QC=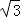 ,MC=1,所以得OM=
,MC=1,所以得OM=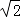 ;
;
在等腰△BCP中,易得PM=1,
所以△PQM是等腰直角三角形,
于是∠PQN=∠PQM=45°.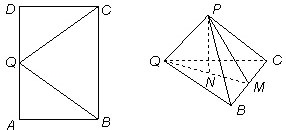

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 已知矩形ABCD中,AB=6,BC=6
已知矩形ABCD中,AB=6,BC=6 如图,在矩形ABCD中,
如图,在矩形ABCD中,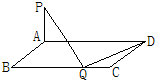 如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥DQ,则a的值等于
如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥DQ,则a的值等于