Question

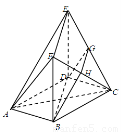
如图，在多面体ABCDEF中，底面ABCD是边长为2的正方形，四边形BDEF是矩形，平面BDEF⊥平面ABCD，BF=3，G和H分别是CE和CF的中点.

（Ⅰ）求证：AC⊥平面BDEF；

（Ⅱ）求证：平面BDGH//平面AEF；

（Ⅲ）求多面体ABCDEF的体积.

 

Answer 1

【答案】

（Ⅰ）答案详见解析；（Ⅱ）答案详见解析；（Ⅲ）.

【解析】

试题分析：（Ⅰ）∵平面平面，且，由面面垂直的性质定理知平面，该题还可以利用线面垂直的判定定理证明，先证平面，得，又，进而证明平面；（Ⅱ）要证明面面平行，需寻求两个线面平行关系，由，得平面；设，连接，则，从而平面，进而证明平面平面；（Ⅲ）对于不规则几何体的体积问题，可以采取割补的办法，将之转化为规则的几何体来求，所求几何体的体积等于.

试题解析：（Ⅰ）证明：因为四边形是正方形，所以.

又因为平面平面，平面平面，且平面，

所以平面.

（Ⅱ）证明：在中，因为分别是的中点，所以，又因为平面，平面，所以平面.设，连接，在中，因为，，所以，又因为平面，平面，所以平面.

又因为，平面，所以平面平面.

（Ⅲ）解：由（Ⅰ），得 平面，，四边形的面积，

所以四棱锥的体积.同理，四棱锥的体积.

所以多面体的体积

考点：1、直线和平面垂直的判定；2、面面平行的判定；3、几何体的体积.