题目内容
若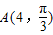
，
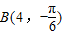，则|AB|= ；S△AOB= ．（其中O是极点）
【答案】分析：根据极坐标的定义，可得|A0|=|B0|=4，且∠A0B=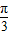
-（-
）=
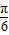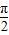，得到等腰Rt△AOB中直角边长为4．由此即可算出斜边AB的长和三角形AOB的面积，得到本题答案．
解答：解：∵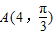
，
，
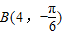∴|A0|=|B0|=4，∠A0B=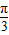
-（-
）=
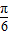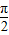
因此，△AOB是直角边长为4的等腰直角三角形
∴|AB|=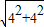
=4
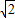，S△AOB=
×|A0|×|B0|=8
故答案为：4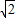
，8
点评：本题给出A、B两点的极坐标，求AB的长和三角形AOB的面积，着重考查了极坐标的认识、勾股定理和三角形面积公式等知识，属于基础题．
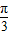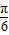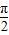-（-）=，得到等腰Rt△AOB中直角边长为4．由此即可算出斜边AB的长和三角形AOB的面积，得到本题答案．解答：解：∵
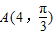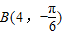，，∴|A0|=|B0|=4，∠A0B=
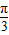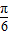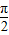
-（-）=因此，△AOB是直角边长为4的等腰直角三角形
∴|AB|=
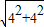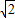=4，S△AOB=×|A0|×|B0|=8故答案为：4
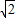，8点评：本题给出A、B两点的极坐标，求AB的长和三角形AOB的面积，着重考查了极坐标的认识、勾股定理和三角形面积公式等知识，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
B”的逆否命题是（ ）
B
B
B,则A∩B≠A
B,则A∩B≠A
距离的和等于定长的点的轨迹是椭圆；
，则
或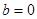
”的逆否命题是“若
且
，则ab≠0”；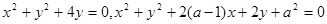
在交点处的切线互相垂直，那么实数
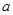的值为
．
α, B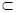
α; ② 若A