题目内容
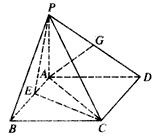
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,PA=AB=4,G为PD中点,E点在AB上,平面PEC⊥平面PDC,
(Ⅰ)求证:AG⊥平面PCD;
(Ⅱ)求证:AG∥平面PEC;
(Ⅲ)求点G到平面PEC的距离。
(Ⅰ)求证:AG⊥平面PCD;
(Ⅱ)求证:AG∥平面PEC;
(Ⅲ)求点G到平面PEC的距离。
| (Ⅰ)证明:∵CD⊥AD,CD⊥PA, ∴CD⊥平面PAD, ∴CD⊥AG, 又PD⊥AG, ∴AG⊥平面PCD; |
|
| (Ⅱ)证明:作EF⊥PC于F, 因面PEC⊥面PCD, ∴EF⊥平面PCD, 又由(Ⅰ)知AG⊥平面PCD, ∴EF∥AG, 又AG 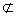 面PEC,EF 面PEC,EF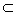 面PEC, 面PEC,∴AG∥平面PEC; |
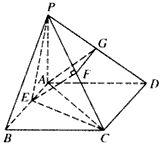 |
| (Ⅲ)解:由AC∥平面PEC知 A,G两点到平面PEC的距离相等, 由(Ⅱ)知A,E,F,G四点共面, 又AE∥CD, ∴AE∥平面PCD,∴AE∥GF, ∴四边形AEFG为平行四边形, ∴AE=GF,PA=AB=4,G为PD中点, 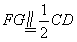 , , ∴FG=2, ∴AE=FG=2, ∴ 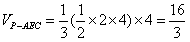 , ,又EF⊥PC,EF=AG= 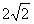 , , ∴ 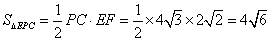 , ,又 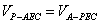 , ,∴ 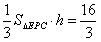 , ,即 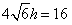 , ,∴h= 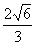 , , ∴G点到平面PEC的距离为 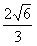 。 。 |

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC. 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a,
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a, 如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点
如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点 (2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.
(2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.