Question

球O与底面边长为3的正三棱柱各侧面均相切，则球的表面积为

3π

．

Answer 1

分析：根据题意，可得球O的半径恰好等于底面正三角形的内切圆半径，由此在底面正△ABC中利用解三角形的知识，算出△ABC的中心到边的距离，得到R=

3

2

，再根据球的表面积公式加以计算，可得答案．

解答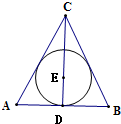：解：球O与一个底面△ABC的切点为E，可得E为底面正△ABC的中心，
∵正三棱柱的底面边长为3，∴△ABC中，高CD=

3

2

AB=

3 3

2

，
可得点E到边的距离为DE=

1

3

CD=

3

2

．
设球O的半径为R，
∵球O与底面边长为3的正三棱柱各侧面均相切，
∴球O的半径等于底面正三角形内切圆半径，即R=DE

3

2

，
因此，球0的表面积为S=4πR²=3π．
故答案为：3π

点评：本题给出以正三棱柱各个面都相切的球，求球的表面积．着重考查了正三棱柱的性质、多面体的内切球、解三角形和球的表面积公式等知识，属于中档题．