题目内容
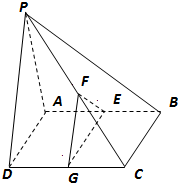 底面是平行四边形的四棱锥P-ABCD,E、F、G分别为AB、PC、DC的中点,
底面是平行四边形的四棱锥P-ABCD,E、F、G分别为AB、PC、DC的中点,(1)求证:EF∥面PAD;
(2)若PA⊥平面ABCD,求证:面EFG⊥面ABCD.
分析:(1)根据线面平行的判定定理证明EF∥面PAD;
(2)根据PA⊥平面ABCD的性质,利用面面垂直的判定定理证明面EFG⊥面ABCD.
(2)根据PA⊥平面ABCD的性质,利用面面垂直的判定定理证明面EFG⊥面ABCD.
解答:解:(1)取PD的中点M,连接AM,连接MF,
则由题意知MF∥DG且MF=DG.
又 DG∥AE且 DG=AE,
∴MF∥AE且 MF=AE,
∴四边形MDGF为平行四边行.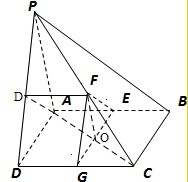
∴EF∥AM.
又EF?平面PAD,MA?平面PAD,
∴EF∥面PAD;
(2)连接AC,交GE于O,连接OF,
则由题意知AO=OC,
又PF=FC,
∴OF∥PA.
又∵PA⊥面ABCD,
∴OF⊥面ABCD,
又∵OF?面EFG,
∴面EFG⊥面ABCD.
则由题意知MF∥DG且MF=DG.
又 DG∥AE且 DG=AE,
∴MF∥AE且 MF=AE,
∴四边形MDGF为平行四边行.

∴EF∥AM.
又EF?平面PAD,MA?平面PAD,
∴EF∥面PAD;
(2)连接AC,交GE于O,连接OF,
则由题意知AO=OC,
又PF=FC,
∴OF∥PA.
又∵PA⊥面ABCD,
∴OF⊥面ABCD,
又∵OF?面EFG,
∴面EFG⊥面ABCD.
点评:本题主要考查线面平行和面面垂直的判定,利用线面平行和面面垂直的判定定理是解决本题的关键,考查学生的推理能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知平行六面体ABCD-A1B1C1D1(底面是平行四边形的四棱柱)
如图,已知平行六面体ABCD-A1B1C1D1(底面是平行四边形的四棱柱)