题目内容
过点Q(-2,
)作圆O:x2+y2=r2(r>0)的切线,切点为D,且QD=4.
(1)求r的值;
(2)设P是圆O上位于第一象限内的任意一点,过点P作圆C的切线l,且l交x轴于点A,交y轴于点B,设
=
+
,求|
|的最小值(O为坐标原点).
(3)从圆O外一点M(x1,y1)向该圆引一条切线,切点为T,N(2,3),且有|MT|=|MN|,求|MT|的最小值,并求此时点M的坐标.
| 21 |
(1)求r的值;
(2)设P是圆O上位于第一象限内的任意一点,过点P作圆C的切线l,且l交x轴于点A,交y轴于点B,设
| OK |
| OA |
| OB |
| OK |
(3)从圆O外一点M(x1,y1)向该圆引一条切线,切点为T,N(2,3),且有|MT|=|MN|,求|MT|的最小值,并求此时点M的坐标.
(1)圆C:x2+y2=r2(r>0)的圆心为O(0,0),则
∵过点Q(-2,
)作圆C:x2+y2=r2(r>0)的切线,切点为D,且QD=4
∴r=OD=
=
=3;
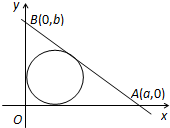
(2)设直线l的方程为
+
=1(a>0,b>0),即bx+ay-ab=0,则A(a,0),B(0,b),
∵
=
+
,∴
=(a,b),∴|
|=
∵直线l与圆C相切,∴
=3
∴3
=ab≤
∴a2+b2≥36
∴|
|≥6
当且仅当a=b=3
时,|
|的最小值为6.
(3)∵切线MN⊥OT,∴|MT|2=|MO|2-9,又|MN|=|MT|,∴|MN|2=|MO|2-9,
M(x1,y1),过N(2,3)的直线的斜率为k,所以NT的方程为:y-3=k(x-2),
与圆的方程x2+y2=9联立,
,消去y可得:(k2+1)x2+2(3-2k)kx+4k2-12k=0,
因为直线与圆相切,所以△=0,即[2(3-2k)k]2-4(k2+1)(4k2-12k)=0,
化简得:5k2+12k=0,解得k=0或k=-
,
当k=0时,x=0,此时T(0,3),当k=
时,x=
,此时T(
,
)
∴满足条件的M点坐标为(1,3)或(
,
)
∵过点Q(-2,
| 21 |
∴r=OD=
| QO2-QD2 |
| 4+21-16 |
(2)设直线l的方程为
| x |
| a |
| y |
| b |

∵
| OK |
| OA |
| OB |
| OK |
| OK |
| a2+b2 |
∵直线l与圆C相切,∴
| |-ab| | ||
|
∴3
| a2+b2 |
| a2+b2 |
| 2 |
∴a2+b2≥36
∴|
| OK |
当且仅当a=b=3
| 2 |
| OK |
(3)∵切线MN⊥OT,∴|MT|2=|MO|2-9,又|MN|=|MT|,∴|MN|2=|MO|2-9,
M(x1,y1),过N(2,3)的直线的斜率为k,所以NT的方程为:y-3=k(x-2),
与圆的方程x2+y2=9联立,
|
因为直线与圆相切,所以△=0,即[2(3-2k)k]2-4(k2+1)(4k2-12k)=0,
化简得:5k2+12k=0,解得k=0或k=-
| 12 |
| 5 |
当k=0时,x=0,此时T(0,3),当k=
| 12 |
| 5 |
| 36 |
| 13 |
| 31 |
| 13 |
| 27 |
| 13 |
∴满足条件的M点坐标为(1,3)或(
| 31 |
| 13 |
| 27 |
| 13 |

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目