题目内容
已知两个不重合的平面α和β,下面给出四个条件:
①α内有无穷多条直线均与平面β平行;
②平面α,β均与平面γ平行;
③平面α,β与平面γ都相交,且其交线平行;
④平面α,β与直线l所成的角相等.
其中能推出α∥β的是
- A.①
- B.②
- C.①和③
- D.③和④
B
分析:α内有无穷多条直线均与平面β平行,这两个平面平行或相交,平面α,β均与平面γ平行,则有α∥β成立,
平面α,β与平面γ都相交,且其交线平行,则平面α,β可能平行,也可能相交,
平面α,β与直线l所成的角相等,则平面α,β可能平行,也可能相交.
解答:①α内有无穷多条直线均与平面β平行,这两个平面平行或相交,故不能推出α∥β,故①不满足条件.
②平面α,β均与平面γ平行,则有α∥β成立,故②满足条件.
③平面α,β与平面γ都相交,且其交线平行,则平面α,β可能平行,也可能相交,故③不满足条件.
④平面α,β与直线l所成的角相等,则平面α,β可能平行,也可能相交,故④不满足条件.
综上,只有②满足条件,
故选 B.
点评:本题考查判定两个平面平行的方法,注意利用两个平面平行的定义和判定定理.
分析:α内有无穷多条直线均与平面β平行,这两个平面平行或相交,平面α,β均与平面γ平行,则有α∥β成立,
平面α,β与平面γ都相交,且其交线平行,则平面α,β可能平行,也可能相交,
平面α,β与直线l所成的角相等,则平面α,β可能平行,也可能相交.
解答:①α内有无穷多条直线均与平面β平行,这两个平面平行或相交,故不能推出α∥β,故①不满足条件.
②平面α,β均与平面γ平行,则有α∥β成立,故②满足条件.
③平面α,β与平面γ都相交,且其交线平行,则平面α,β可能平行,也可能相交,故③不满足条件.
④平面α,β与直线l所成的角相等,则平面α,β可能平行,也可能相交,故④不满足条件.
综上,只有②满足条件,
故选 B.
点评:本题考查判定两个平面平行的方法,注意利用两个平面平行的定义和判定定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 和两条不同直线
和两条不同直线 ,则下列说法正确的是( )
,则下列说法正确的是( ) 则
则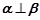
 则
则
 则
则 则
则