题目内容
已知非零向量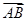 与
与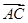 满足
满足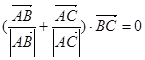 且
且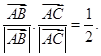 则
则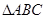 为( )
为( )
| A.等边三角形 | B.直角三角形 |
| C.等腰非等边三角形 | D.三边均不相等的三角形 |
A
解析试题分析:因为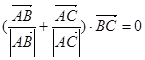 ,所以
,所以 (其中
(其中 是平分
是平分 的单位向量),
的单位向量),
又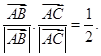 ,所以
,所以 ,所以三角形是等边三角形.故选A.
,所以三角形是等边三角形.故选A.
考点:向量的数量积运算
点评:本题考查了向量的数量积运算,解题的关键是运算和明白向量的几何意义,属中档题.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
已知平面向量 ,
, ,满足
,满足 ,
, ,
, ,则
,则 =( )
=( )
| A.2 | B.3 | C.4 | D.6 |
已知平面向量a、b均为单位向量,且a与b的夹角为1200,则|2a+b|=( )
| A.3 | B.7 | C.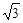 | D. |
已知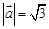 ,
,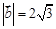 ,
,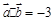 ,则
,则 与
与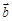 的夹角是
的夹角是
A.30 | B.60 | C.120 | D.150 |
空间四边形 中,
中, ,
, ,则
,则 <
< >的值是( )
>的值是( )
A. | B. | C.- | D. |
如图,AB是圆O的直径,P是圆弧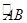 上的点,M,N是直径AB上关于O对称的两点,且
上的点,M,N是直径AB上关于O对称的两点,且 ,则
,则
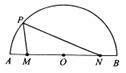
| A.13 | B.7 | C.5 | D.3 |
在Rt 中,
中, ( )
( )
A.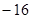 | B.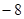 | C.8 | D.16 |
已知非零向量 、
、 满足
满足 ,那么向量
,那么向量 与向量
与向量 的夹角为( )
的夹角为( )
A. | B. | C. | D. |
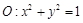 和三点,
和三点, ,
,
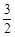 B.
B. C.
C.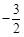 D.
D.