题目内容
已知平面向量 =(cosψ,sinψ),
=(cosψ,sinψ),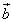 =(cosx,sinx),
=(cosx,sinx),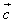 =(sinψ,-cosψ),其中0<ψ<π,且函数f(x)=(
=(sinψ,-cosψ),其中0<ψ<π,且函数f(x)=(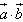 )cosx+(
)cosx+(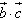 )sinx的图象过点(
)sinx的图象过点(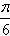 ,1)。
,1)。
(1)求ψ的值;
(2)将函数y=f(x)图象上各点的横坐标变为原来的的2倍,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)在[0, ]上的最大值和最小值。
]上的最大值和最小值。
 =(cosψ,sinψ),
=(cosψ,sinψ),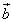 =(cosx,sinx),
=(cosx,sinx),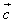 =(sinψ,-cosψ),其中0<ψ<π,且函数f(x)=(
=(sinψ,-cosψ),其中0<ψ<π,且函数f(x)=(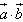 )cosx+(
)cosx+(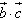 )sinx的图象过点(
)sinx的图象过点(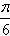 ,1)。
,1)。(1)求ψ的值;
(2)将函数y=f(x)图象上各点的横坐标变为原来的的2倍,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)在[0,
 ]上的最大值和最小值。
]上的最大值和最小值。解:(1)∵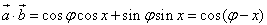
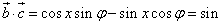
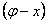
∴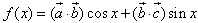
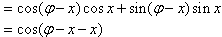
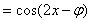
即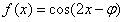
∴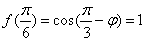
而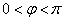
∴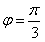 。
。
(2)由(1)得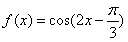
于是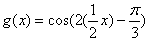
即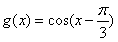
当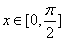 时,
时,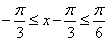
所以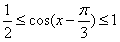
即当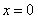 时,
时,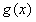 取最小值
取最小值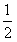
当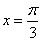 时,
时,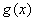 取得最大值1。
取得最大值1。
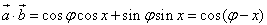
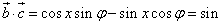
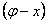
∴
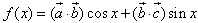
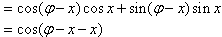
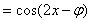
即
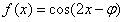
∴
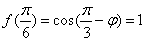
而
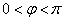
∴
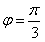 。
。(2)由(1)得
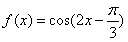
于是
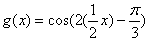
即
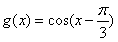
当
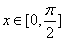 时,
时,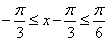
所以
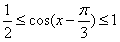
即当
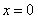 时,
时,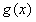 取最小值
取最小值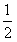
当
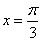 时,
时,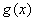 取得最大值1。
取得最大值1。
练习册系列答案
相关题目