题目内容
设命题P:函数y=loga(x+1)在(0,+∞)为减函数.命题Q:曲线y=x2+(2a-3)x+1与x轴有两个不同的交点.若“P且Q”为假,“P或Q”为真,求a的范围.
分析:当P为真时,0<a<1.当Q为真时,a>
或a<
.当P为真、Q为假时,求出a的范围;当P为假、Q为真时,
求出a的范围,把这几个a的范围取并集即得所求.
| 5 |
| 2 |
| 1 |
| 2 |
求出a的范围,把这几个a的范围取并集即得所求.
解答:解:当P为真时,0<a<1.当Q为真时,△=(2a-3)2-4>0,即 a>
或a<
.
∵“P且Q”为假,“P或Q”为真,∴P与Q必是一真一假.
当P为真、Q为假时,则有
,解得
≤a<1.
当P为假、Q为真时,则有
,解得a>
或a≤0.
综上可得
≤a<1或a≤0或a>
.
| 5 |
| 2 |
| 1 |
| 2 |
∵“P且Q”为假,“P或Q”为真,∴P与Q必是一真一假.
当P为真、Q为假时,则有
|
| 1 |
| 2 |
当P为假、Q为真时,则有
|
| 5 |
| 2 |
综上可得
| 1 |
| 2 |
| 5 |
| 2 |
点评:本题主要考查对数函数的单调性和特殊点,复合命题的真假,二次函数的性质,属于中档题.

练习册系列答案
相关题目
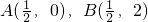 及直线
及直线 的距离相等,那么满足条件的点P有且只有1个.
的距离相等,那么满足条件的点P有且只有1个.