题目内容
 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.
(Ⅰ)证明:A1C⊥平面BED;
(Ⅱ)(理)求二面角A1-DE-B的大小.
(文)异面直线A1C与AB所成的角.
解:
以D为坐标原点,射线DA为x轴的正半轴,
建立如图所示直角坐标系D-xyz.
依题设,B(2,2,0),C(0,2,0),E(0,2,1),A1(2,0,4).
 ,
, .
.
(Ⅰ)因为 ,
, ,A1C⊥BD,A1C⊥DE.
,A1C⊥BD,A1C⊥DE.
又DB∩DE=D,
所以A1C⊥平面DBE.
(Ⅱ)(理)设向量n=(x,y,z)是平面DA1E的法向量,则 ,
, .
.
故2y+z=0,2x+4z=0.
令y=1,则z=-2,x=4,n=(4,1,-2). 等于二面角A1-DE-B的平面角,
等于二面角A1-DE-B的平面角, .
.
所以二面角A1-DE-B的大小为 .
.
(文)
∴
∴异面直线A1C与AB所成的角为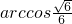 .
.
分析:(Ⅰ)以D为坐标原点,射线DA为x轴的正半轴,建立空间直角坐标系D-xyz.用坐标表示向量,从而可证 ,
, ,故有A1C⊥平面DBE.
,故有A1C⊥平面DBE.
(Ⅱ)先求平面的法向量,利用向量n=(x,y,z)是平面DA1E的法向量,则 ,
, .再用向量的夹角公式求解即可
.再用向量的夹角公式求解即可
(文) 再用向量的夹角公式求解即可求异面直线A1C与AB所成的角.
再用向量的夹角公式求解即可求异面直线A1C与AB所成的角.
点评:本题以正四棱柱为载体,考查线面位置关系,考查线线角,面面角,关键是构建空间直角坐标系.

以D为坐标原点,射线DA为x轴的正半轴,
建立如图所示直角坐标系D-xyz.
依题设,B(2,2,0),C(0,2,0),E(0,2,1),A1(2,0,4).
 ,
, .
.(Ⅰ)因为
 ,
, ,A1C⊥BD,A1C⊥DE.
,A1C⊥BD,A1C⊥DE.又DB∩DE=D,
所以A1C⊥平面DBE.
(Ⅱ)(理)设向量n=(x,y,z)是平面DA1E的法向量,则
 ,
, .
.故2y+z=0,2x+4z=0.
令y=1,则z=-2,x=4,n=(4,1,-2).
 等于二面角A1-DE-B的平面角,
等于二面角A1-DE-B的平面角, .
.所以二面角A1-DE-B的大小为
 .
.(文)

∴

∴异面直线A1C与AB所成的角为
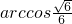 .
.分析:(Ⅰ)以D为坐标原点,射线DA为x轴的正半轴,建立空间直角坐标系D-xyz.用坐标表示向量,从而可证
 ,
, ,故有A1C⊥平面DBE.
,故有A1C⊥平面DBE.(Ⅱ)先求平面的法向量,利用向量n=(x,y,z)是平面DA1E的法向量,则
 ,
, .再用向量的夹角公式求解即可
.再用向量的夹角公式求解即可(文)
 再用向量的夹角公式求解即可求异面直线A1C与AB所成的角.
再用向量的夹角公式求解即可求异面直线A1C与AB所成的角.点评:本题以正四棱柱为载体,考查线面位置关系,考查线线角,面面角,关键是构建空间直角坐标系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
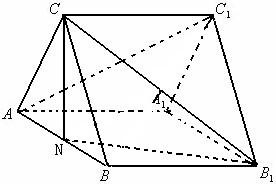 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
