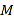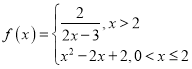题目内容
【题目】若函数![]() 对定义城内的每一个值
对定义城内的每一个值![]() ,在其定义域内都存在唯一的
,在其定义域内都存在唯一的![]() ,使得
,使得![]() 成立,则称该函数为“
成立,则称该函数为“![]() 函数”.
函数”.
(1)判断函数![]() 是否为“
是否为“![]() 函数”,并说明理由;
函数”,并说明理由;
(2)若函数![]() 在定义域
在定义域![]() 上为“
上为“![]() 函数”,求
函数”,求![]() 的取值范围;
的取值范围;
(3)已知函数![]() 在定义域
在定义域![]() 上为“
上为“![]() 函数”.若存在实数
函数”.若存在实数![]() ,使得对任意的
,使得对任意的![]() ,不等式
,不等式![]() 都成立,求实数
都成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)不是,理由见解析;
(2)![]() ;
;
(3)![]() 或
或![]() ;
;
【解析】
(1)通过列举的方式可判断不是反函数;
(2)由函数![]() 在定义域
在定义域![]() 上为“
上为“![]() 函数”可得
函数”可得![]() ,
,![]() ,
,
![]() 可代换为
可代换为![]() ,结合导数可求得范围;
,结合导数可求得范围;
(3)由“![]() 函数”定义可先求证函数在
函数”定义可先求证函数在![]() 上单调,且
上单调,且![]() ,求得参数
,求得参数![]() ,由
,由![]() 对于任意实数
对于任意实数![]() 恒成立整理得
恒成立整理得![]() ,变形成关于
,变形成关于![]() 的二次不等式
的二次不等式![]() ,再令
,再令![]() 进一步求得
进一步求得![]() 值即可
值即可
(1)![]() 不是为“
不是为“![]() 函数”.
函数”.
若![]() ,当
,当![]() 或
或![]() 时,满足
时,满足![]() ,
,
此时![]() 不唯一,所以
不唯一,所以![]() 不是为“
不是为“![]() 函数”.
函数”.
(2)因为函数![]() 在
在![]() 为増函数,且在
为増函数,且在![]() 上为“
上为“![]() 函数”,
函数”,
所以![]() ,即
,即![]() .
.
又因为![]() ,所以
,所以![]() .
.
所以![]() .
.
令![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,即
,即![]() .
.
(3)若![]() 图像对称轴
图像对称轴![]() ,设
,设![]() ,且
,且![]() ,
,![]() 关于
关于![]() 对称,
对称,
此时,![]() ,由条件可知,存在
,由条件可知,存在![]() ,使
,使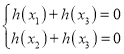 ,这与“
,这与“![]() 函数”定义矛盾.
函数”定义矛盾.
所以![]() 在
在![]() 上单调,且
上单调,且![]() ,
,
由![]() ,得
,得![]() ,解得
,解得![]() 或
或![]() .
.
检验:![]() 在
在![]() 上单调,所以
上单调,所以![]() .
.
不等式即![]() ,
,
整理得![]() ,由题意知,上式对任意
,由题意知,上式对任意![]() 恒成立.
恒成立.
得![]() ,
,
整理得![]() ,由题意知,存在
,由题意知,存在![]() 使得上式成立,
使得上式成立,
所以![]() 或
或![]() .
.
解得![]() 或
或![]() .
.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目