题目内容
市民李生居住在甲地,工作在乙地,他的小孩就读的小学在丙地,三地之间的道路情况如图所示.假设工作日不走其它道路,只在图示的道路中往返,每次在路口选择道路是随机的.同一条道路去程与回程是否堵车相互独立.假设李生早上需要先开车送小孩去丙地小学,再返回经甲地赶去乙地上班.假设道路A、B、D上下班时间往返出现拥堵的概率都是 ,道路C、E上下班时间往返出现拥堵的概率都是
,道路C、E上下班时间往返出现拥堵的概率都是 ,只要遇到拥堵上学和上班的都会迟到.
,只要遇到拥堵上学和上班的都会迟到.

(1)求李生小孩按时到校的概率;
(2)李生是否有七成把握能够按时上班?
(3)设ξ表示李生下班时从单位乙到达小学丙遇到拥堵的次数,求ξ的均值.
解:(1)因为道路D、E上班时间往返出现拥堵的概率分别是 和
和 .
.
因此从甲到丙遇到拥堵的概率是 ,
,
所以李生小孩能够按时到校的概率是1-0.15=0.85;
(2)甲到丙没有遇到拥堵的概率是 ,
,
丙到甲没有遇到拥堵的概率也是 ,
,
甲到乙遇到拥堵的概率是 ,
,
甲到乙没有遇到拥堵的概率是 ,
,
∴李生上班途中均没有遇到拥堵的概率是 ,所以李生没有七成把握能够按时上班.
,所以李生没有七成把握能够按时上班.
(3)依题意ξ可以取0,1,2.
P(ξ=0)= ,P(ξ=1)=
,P(ξ=1)= ,P(ξ=2)=
,P(ξ=2)= .
.
分布列是:Eξ= =
=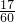
分析:(1)先求出从甲到丙遇到拥堵的概率,利用对立事件的概率计算公式即可得到李生小孩能够按时到校的概率;
(2)由(1)的结论可得:甲到丙没有遇到拥堵的概率是 ,同样丙到甲没有遇到拥堵的概率也是
,同样丙到甲没有遇到拥堵的概率也是 ;先求出:甲到乙遇到拥堵的概率,由对立事件的概率即可得到甲到乙没有遇到拥堵的概率,利用独立事件的概率计算公式即可得到李生上班途中均没有遇到拥堵的概率,即可判断出答案.
;先求出:甲到乙遇到拥堵的概率,由对立事件的概率即可得到甲到乙没有遇到拥堵的概率,利用独立事件的概率计算公式即可得到李生上班途中均没有遇到拥堵的概率,即可判断出答案.
(3)利用(1)(2)的结论和独立事件的概率计算公式和互斥事件的概率计算公式即可得出,再利用分布列和数学期望即可得出.
点评:正确理解题意和熟练掌握独立事件、对立事件、互斥事件的概率计算公式和分布列、数学期望的计算公式是解题的关键.
 和
和 .
.因此从甲到丙遇到拥堵的概率是
 ,
,所以李生小孩能够按时到校的概率是1-0.15=0.85;
(2)甲到丙没有遇到拥堵的概率是
 ,
,丙到甲没有遇到拥堵的概率也是
 ,
,甲到乙遇到拥堵的概率是
 ,
,甲到乙没有遇到拥堵的概率是
 ,
,∴李生上班途中均没有遇到拥堵的概率是
 ,所以李生没有七成把握能够按时上班.
,所以李生没有七成把握能够按时上班.(3)依题意ξ可以取0,1,2.
P(ξ=0)=
 ,P(ξ=1)=
,P(ξ=1)= ,P(ξ=2)=
,P(ξ=2)= .
.| ξ | 0 | 1 | 2 |
| P |  |  |  |
 =
=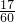
分析:(1)先求出从甲到丙遇到拥堵的概率,利用对立事件的概率计算公式即可得到李生小孩能够按时到校的概率;
(2)由(1)的结论可得:甲到丙没有遇到拥堵的概率是
 ,同样丙到甲没有遇到拥堵的概率也是
,同样丙到甲没有遇到拥堵的概率也是 ;先求出:甲到乙遇到拥堵的概率,由对立事件的概率即可得到甲到乙没有遇到拥堵的概率,利用独立事件的概率计算公式即可得到李生上班途中均没有遇到拥堵的概率,即可判断出答案.
;先求出:甲到乙遇到拥堵的概率,由对立事件的概率即可得到甲到乙没有遇到拥堵的概率,利用独立事件的概率计算公式即可得到李生上班途中均没有遇到拥堵的概率,即可判断出答案.(3)利用(1)(2)的结论和独立事件的概率计算公式和互斥事件的概率计算公式即可得出,再利用分布列和数学期望即可得出.
点评:正确理解题意和熟练掌握独立事件、对立事件、互斥事件的概率计算公式和分布列、数学期望的计算公式是解题的关键.

练习册系列答案
相关题目
 (2013•江门二模)市民李生居住在甲地,工作在乙地,他的小孩就读的小学在丙地,三地之间的道路情况如图所示.假设工作日不走其它道路,只在图示的道路中往返,每次在路口选择道路是随机的.同一条道路去程与回程是否堵车互不影响.假设李生早上需要先开车送小孩去丙地小学,再返回经甲地赶去乙地上班,
(2013•江门二模)市民李生居住在甲地,工作在乙地,他的小孩就读的小学在丙地,三地之间的道路情况如图所示.假设工作日不走其它道路,只在图示的道路中往返,每次在路口选择道路是随机的.同一条道路去程与回程是否堵车互不影响.假设李生早上需要先开车送小孩去丙地小学,再返回经甲地赶去乙地上班,

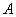 、
、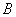 、
、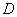 上下班时间往返出现拥堵的概率都是
上下班时间往返出现拥堵的概率都是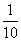 ,
,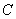 、
、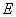 上下班时间往返出现拥堵的概率都是
上下班时间往返出现拥堵的概率都是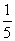 ,只要遇到拥堵上学和上班的都会迟到.
,只要遇到拥堵上学和上班的都会迟到.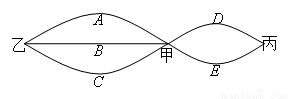
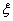 表示李生下班时从单位乙到达小学丙遇到拥堵的次数,求
表示李生下班时从单位乙到达小学丙遇到拥堵的次数,求