题目内容
18.经过抛物线y2=2px(p≠0)的顶点O作两条弦OA和OB,若弦OA、OB的斜率k1,k2恰好是方程x2+6x-4=0的两个根,则直线AB的斜率为$\frac{2}{3}$.分析 求出A,B的坐标,可得直线AB的斜率为k=$\frac{{k}_{1}{k}_{2}}{{k}_{1}+{k}_{2}}$,利用韦达定理,即可得出结论.
解答 解:依题意设直线OA的方程为y=k1x与y2=2px,联立解得A($\frac{2p}{{{k}_{1}}^{2}}$,$\frac{2p}{{k}_{1}}$),
同理B($\frac{2p}{{{k}_{2}}^{2}}$,$\frac{2p}{{k}_{2}}$)
∴直线AB的斜率为k=$\frac{{k}_{1}{k}_{2}}{{k}_{1}+{k}_{2}}$,
∵弦OA、OB的斜率k1,k2恰好是方程x2+6x-4=0的两个根,
∴k1+k2=-6,k1k2=-4,
∴k=$\frac{{k}_{1}{k}_{2}}{{k}_{1}+{k}_{2}}$=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题考查直线与抛物线的位置关系,考查韦达定理的运用,属于中档题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
8.2015年12月10日开始,武汉淹没在白色雾霾中,PM2.5浓度在200微克~300微克/立方米的范围,空气质量维持重度污染.某兴趣小组欲研究武昌区PM2.5浓度大小与患鼻炎人数多少之前的关系,他们分别到气象局与该地区某医院抄录了12月10日至15日的武昌区PM2.5浓度大小与该地区因患鼻炎而就诊的人数,整理得到如下资料:
该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行实验.
(Ⅰ)若选取的是10号与15号的两组数据,请根据11至14号的数据,求出y关于x的线性回归方程;附:对于一组数据(x1,y1),(x2,y2),…(xn,yn),其回归直线$\widehat{y}$=$\widehat{a}$+$\widehat{b}$x的斜率和截距的最小二乘估计分别为:$\stackrel{∧}{b}=\frac{\sum_{i=1}^{n}({y}_{i}-\overline{y})({x}_{i}-\overline{x})}{\sum_{i=1}^{n}{({x}_{i}-\overline{x})}^{2}},\stackrel{∧}{a}=\overline{y}-\stackrel{∧}{b}\overline{x}$
(Ⅱ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性方程是理想的,该问该小组所得线性回归方程是否理想?
| 日期 | 12月10日 | 12月11日 | 12月12日 | 12月13日 | 12月14日 | 12月15日 |
| PM2.5浓度 超过200的部分为x (微克/立方米) | 10 | 11 | 13 | 12 | 8 | 5 |
| 就诊人数y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
(Ⅰ)若选取的是10号与15号的两组数据,请根据11至14号的数据,求出y关于x的线性回归方程;附:对于一组数据(x1,y1),(x2,y2),…(xn,yn),其回归直线$\widehat{y}$=$\widehat{a}$+$\widehat{b}$x的斜率和截距的最小二乘估计分别为:$\stackrel{∧}{b}=\frac{\sum_{i=1}^{n}({y}_{i}-\overline{y})({x}_{i}-\overline{x})}{\sum_{i=1}^{n}{({x}_{i}-\overline{x})}^{2}},\stackrel{∧}{a}=\overline{y}-\stackrel{∧}{b}\overline{x}$
(Ⅱ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性方程是理想的,该问该小组所得线性回归方程是否理想?
9.i是虚数单位,复数$\frac{2i}{z}=-1+i$,则z的共轭复数是( )
| A. | -1+i | B. | -i+1 | C. | i+1 | D. | -i-1 |
 如图,将一个边长为2cm和5cm,两邻边夹角为60°的平行四边形绕其5cm边上的高所在直线旋转一周形成的几何体是圆台.
如图,将一个边长为2cm和5cm,两邻边夹角为60°的平行四边形绕其5cm边上的高所在直线旋转一周形成的几何体是圆台.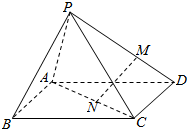 如图,设P为长方形ABCD所在平面外一点,M在PD上,N在AC上,若$\frac{DM}{MP}$=$\frac{CN}{NA}$,用向量法证明:直线MN∥平面PAB.
如图,设P为长方形ABCD所在平面外一点,M在PD上,N在AC上,若$\frac{DM}{MP}$=$\frac{CN}{NA}$,用向量法证明:直线MN∥平面PAB. 一个容量为200的样本频率分布直方图如图所示,则样本数据落在范围[5,9)的频率和频数分别为0.2和180.
一个容量为200的样本频率分布直方图如图所示,则样本数据落在范围[5,9)的频率和频数分别为0.2和180.