题目内容
已知函数f(x)=abx的图象过点A(4,(1)求函数f(x)的解析式;
(2)记an=log2f(n),n 是正整数,Sn是数列{an}的前n项和,解关于n的不等式an·Sn≤0;
(3)对于(2)中的an与Sn,整数96是否为数列{anSn}中的项?若是,求出相应的项数;若不是,说明理由.
解:(1)由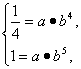 得
得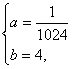
故f(x)=![]() .
.
(2)由题意an=log2(![]() ·4n)=2n-10,Sn=
·4n)=2n-10,Sn=![]() (a1+an)=n(n-9),anSn=2n(n-5)(n-9).
(a1+an)=n(n-9),anSn=2n(n-5)(n-9).
由anSn≤0,得(n-5)(n-9)≤0,即5≤n≤9.
故n=5,6,7,8,9.
(3)a1S1=64,a2S2=84,a3S3=72,a4S4=40.
当5≤n≤9时,anSn≤0;
当n≥10时,anSn≥a10a10=100.
∴96不是数列{anSn}中的项.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
已知函数f(x)=a-
,若f(x)为奇函数,则a=( )
| 1 |
| 2x+1 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |