题目内容
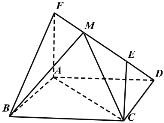
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动,且
上运动,且![]() .
.
(1)当![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)设平面![]() 与平面
与平面![]() 所成二面角的大小为
所成二面角的大小为![]() (
(![]() ),求
),求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)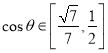
【解析】
(1)证明![]() 平面
平面![]() ,建立空间直角坐标系,写出向量的坐标,
,建立空间直角坐标系,写出向量的坐标,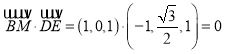 ,故可得
,故可得![]() ,即可求出异面直线
,即可求出异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)设![]() ,利用向量表示出两个平面法向量的夹角余弦
,利用向量表示出两个平面法向量的夹角余弦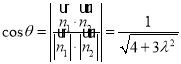 ,根据
,根据![]() ,即可求得求
,即可求得求![]() 的取值范围.
的取值范围.
(1)在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
![]()
![]() ,即
,即![]() .
.
![]() 四边形
四边形![]() 为矩形,故
为矩形,故![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() .
.
建立如图所示的空间直角坐标系,

则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
当![]() 时,
时,![]() ,
,
![]()
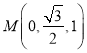 ,可得
,可得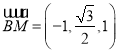 ,
,
又![]()
![]() ,
,
![]()
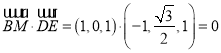
![]()
![]() ,即异面直线
,即异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .
.
(2)平面![]() 的一个法向量
的一个法向量![]() ,
,
设![]() ,
,
由![]()
![]() ,
,
得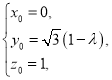 即
即![]() ,
,
![]()
![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() ,
,
![]()
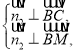 即
即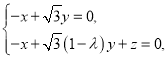
取![]() ,则
,则![]() ,
,![]()
![]() 平面
平面![]() 的一个法向量
的一个法向量![]() ,因为
,因为![]() ,所以
,所以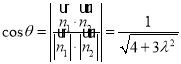 .
.
因为![]() ,所以
,所以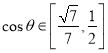 .
.

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案【题目】改革开放以来,伴随着我国经济持续增长,户均家庭教育投入![]() 户均家庭教育投入是指一个家庭对家庭成员教育投入的总和
户均家庭教育投入是指一个家庭对家庭成员教育投入的总和![]() 也在不断提高
也在不断提高![]() 我国某地区2012年至2018年户均家庭教育投入
我国某地区2012年至2018年户均家庭教育投入![]() 单位:千元
单位:千元![]() 的数据如表:
的数据如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
户均家庭教育投入y |
|
|
|
|
|
|
|
![]() 求y关于t的线性回归方程;
求y关于t的线性回归方程;
![]() 利用
利用![]() 中的回归方程,分析2012年至2018年该地区户均家庭教育投入的变化情况,并预测2019年该地区户均家庭教育投入是多少.
中的回归方程,分析2012年至2018年该地区户均家庭教育投入的变化情况,并预测2019年该地区户均家庭教育投入是多少.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: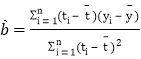 ,
,![]() .
.
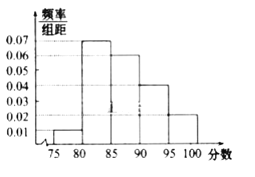
【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
频数 | 6 | 26 | 38 | 22 | 8 |
(I)在答题卡上作出这些数据的频率分布直方图:

(II)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(III)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?