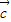题目内容
若方程x2+ax+b=0的两根分别为sinθ和cosθ，则点（a，b）的轨迹是
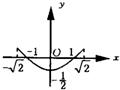
- A.
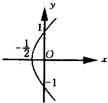
- B.
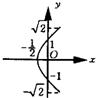
- C.
- D.
B
分析：由一元二次方程根与系数的关系得到a，b与参数θ的关系式，再利用三角函数的同角关系消去参数θ得到关于a，b的普通方程，最后由此方程即可选出答案．
解答：∵方程x2+ax+b=0的两根分别为sinθ和cosθ，
∴由根与系数的关系得：
消去θ得：1+2b=a2，且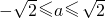
，
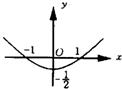
故点（a，b）的轨迹是一段开口向上的抛物线．
故选B．
点评：本题主要考查了轨迹方程的求法、函数的图象以及一元二次方程根与系数的关系，属于基础题．
分析：由一元二次方程根与系数的关系得到a，b与参数θ的关系式，再利用三角函数的同角关系消去参数θ得到关于a，b的普通方程，最后由此方程即可选出答案．
解答：∵方程x2+ax+b=0的两根分别为sinθ和cosθ，
∴由根与系数的关系得：
消去θ得：1+2b=a2，且
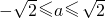，故点（a，b）的轨迹是一段开口向上的抛物线．
故选B．
点评：本题主要考查了轨迹方程的求法、函数的图象以及一元二次方程根与系数的关系，属于基础题．
练习册系列答案
相关题目
若方程x2+ax+b=0有不小于2的实根，则a2+b2的最小值为（ ）
| A、3 | ||
B、
| ||
C、
| ||
D、
|
下面使用类比推理正确的是（ ）
A、直线
| ||||||||||||||||||||||||||||||||||||
| B、同一平面内，直线a，b，c，若a⊥c，b⊥c，则a∥b．类推出：空间中，直线a，b，c，若a⊥c，b⊥c，则a∥b | ||||||||||||||||||||||||||||||||||||
| C、实数a，b，若方程x2+ax+b=0有实数根，则a2≥4b．类推出：复数a，b，若方程x2+ax+b=0有实数根，则a2≥4b | ||||||||||||||||||||||||||||||||||||
| D、以点（0，0）为圆心，r为半径的圆的方程为x2+y2=r2．类推出：以点（0，0，0）为球心，r为半径的球的方程为x2+y2+z2=r2 |
，
，
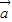，若
∥
，
∥
，则
∥
．类推出：向量
，
，
，若
∥
，
∥
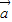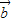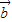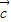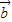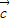，则
∥