题目内容
下列说法正确的是
- A.函数
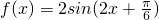 图象的一条对称轴是直线x=
图象的一条对称轴是直线x=
- B.若命题p:“?x∈R,x2-2x-1>0”,则命题¬p:“?x∈R,x2-2x-1<0”
- C.“a=1”是“直线x-ay=0与直线x+ay=0互相垂直”的充要条件
- D.若x≠0,x
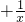 ≥2
≥2
A
分析:对于A,可求得其对称轴方程为x=kπ+ ,k∈Z,从而可作出判断;
,k∈Z,从而可作出判断;
对于B,利用特称命题的否定是全称命题,即可作出判断;
对于C,直线x-ay=0与直线x+ay=0互相垂直,可求得a的值,从而可作出判断;
对于D,利用双钩函数的性质可作出判断.
解答:对于A,,∵函数f(x)=2sin(2x+ ),
),
∴其对称轴方程由2x+ =2kπ+
=2kπ+ ,k∈Z得:x=kπ+
,k∈Z得:x=kπ+ ,k∈Z,
,k∈Z,
显然,当k=0时,x= ,
,
∴A正确;
对于B,命题p:“?x∈R,x2-2x-1>0”,则命题¬p:“?x∈R,x2-2x-1≤0”,故B错误;
对于C,∵直线x-ay=0与直线x+ay=0互相垂直,
∴1-a2=0,
∴a=±1,
故C错误;
对于D,∵x≠0,y=x+ ,
,
∴当x>0时,y≥2,
当x<0时,y≤-2,
故D错误.
故选:A.
点评:本题考查命题的真假判断与应用,考查必要条件、充分条件与充要条件的判断,考查空间中直线与直线之间的位置关系,属于中低档提.
分析:对于A,可求得其对称轴方程为x=kπ+
 ,k∈Z,从而可作出判断;
,k∈Z,从而可作出判断;对于B,利用特称命题的否定是全称命题,即可作出判断;
对于C,直线x-ay=0与直线x+ay=0互相垂直,可求得a的值,从而可作出判断;
对于D,利用双钩函数的性质可作出判断.
解答:对于A,,∵函数f(x)=2sin(2x+
 ),
),∴其对称轴方程由2x+
 =2kπ+
=2kπ+ ,k∈Z得:x=kπ+
,k∈Z得:x=kπ+ ,k∈Z,
,k∈Z,显然,当k=0时,x=
 ,
,∴A正确;
对于B,命题p:“?x∈R,x2-2x-1>0”,则命题¬p:“?x∈R,x2-2x-1≤0”,故B错误;
对于C,∵直线x-ay=0与直线x+ay=0互相垂直,
∴1-a2=0,
∴a=±1,
故C错误;
对于D,∵x≠0,y=x+
 ,
,∴当x>0时,y≥2,
当x<0时,y≤-2,
故D错误.
故选:A.
点评:本题考查命题的真假判断与应用,考查必要条件、充分条件与充要条件的判断,考查空间中直线与直线之间的位置关系,属于中低档提.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则下列说法正确的是( )
,则下列说法正确的是( ) 有且只有一个零点
B.
有且只有一个零点
B. ,
, ,则下列说法正确的是( )
,则下列说法正确的是( )
 ,乙比甲成绩稳定,应该选乙参加比赛
,乙比甲成绩稳定,应该选乙参加比赛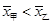 ,甲比乙成绩稳定,应该选甲参加比赛
,甲比乙成绩稳定,应该选甲参加比赛 :函数
:函数 (
( 且
且 )的图像恒过点
)的图像恒过点 ;
; :函数
:函数 有两个零点.
有两个零点.  为假命题 D.
为假命题 D. 为真命题
为真命题 的导函数
的导函数 的图象如上图所示,则下列说法正确的是 ( )
的图象如上图所示,则下列说法正确的是 ( ) 内单调递减 B、函数
内单调递减 B、函数 内单调递增
内单调递增 处取极大值 D、函数
处取极大值 D、函数 处取极小值
处取极小值