题目内容
函数f(x)＝x2＋x－
.
(1)若定义域为[0,3]，求f(x)的值域；
(2)若f(x)的值域为[－
，
]，且定义域为[a，b]，求b－a的最大值.
∵f(x)＝(x＋)2－，
∴对称轴
为x＝－.
(1)∵3≥x≥0>－，
∴f(x)的值域为[f(0)，f(3)]，即[－，
]；
(2)∵x＝－时，f(x)＝－是f(x)的最小值，
∴x＝－∈[a，b]，令x2＋x－＝，
得x1＝－
，x2＝，
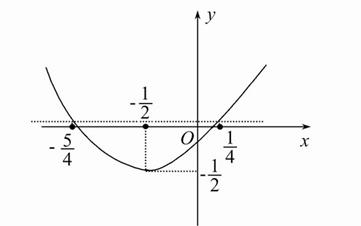
根据f(x)的图象知b－a的最大值是－(－)＝
.
练习册系列答案
相关题目
－1(－3≤x≤3)．
，设函数f(x)＝(x2－2)?(x－x2)，x∈R，若函数y＝f(x)－c的图象与x轴恰有两个公共点，则实数c的取值范围是
B．
D．(－∞，－2]∪