题目内容
已知椭圆C1: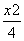 +y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率.
+y2=1,椭圆C2以C1的长轴为短轴,且与C1有相同的离心率.
(1)求椭圆C2的方程;
(2)设O为坐标原点,点A,B分别在椭圆C1和C2上,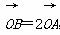 ,求直线AB的方程.
,求直线AB的方程.
解 (1)由已知可设椭圆C2的方程为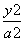 +
+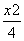 =1(a>2).
=1(a>2).
其离心率为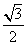 ,故
,故 =
=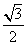 ,解得a=4.
,解得a=4.
故椭圆C2的方程为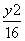 +
+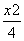 =1.
=1.
(2)A,B两点的坐标分别记为(xA,yA),(xB,yB),
由 =2
=2 及(1)知,O,A,B三点共线且点A,B不在y轴上,因此可设直线AB的方程为y=kx.
及(1)知,O,A,B三点共线且点A,B不在y轴上,因此可设直线AB的方程为y=kx.
将y=kx代入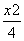 +y2=1中,得(1+4k2)x2=4,
+y2=1中,得(1+4k2)x2=4,
所以x =
= .
.
将y=kx代入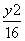 +
+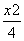 =1中,得(4+k2)x2=16,
=1中,得(4+k2)x2=16,
所以x =
= .又由
.又由 =2
=2  ,得x
,得x =4x
=4x ,即
,即 ,解得k=±1.故直线AB的方程为y=x或y=-x.
,解得k=±1.故直线AB的方程为y=x或y=-x.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
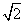 -4 B.
-4 B.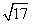 -1 C.6-2
-1 C.6-2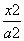 +
+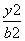 =1(a>b>0)上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是 ( ).
=1(a>b>0)上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是 ( ).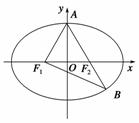 A.
A.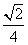 B.
B.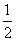 C.
C.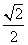 D.
D.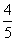 ,则C的离心率为( ).
,则C的离心率为( ). A.
A.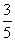 B.
B.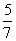 C.
C.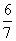
 上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( ).
上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( ). 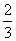 C.
C.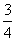 D.
D. ,则双曲线C1:
,则双曲线C1: =1与C2:
=1与C2: =1的( ).
=1的( ).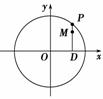 如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=
如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|= |PD|.
|PD|.