题目内容

若函数y=f（x）为偶函数，且在（0，+∞）上是减函数，又f（3）=0，则
f(x)+f(-x)
2x
＜0的解集为（　　）
分析：利用函数的奇偶性将不等式进行化简，然后利用函数的单调性确定不等式的解集．
解答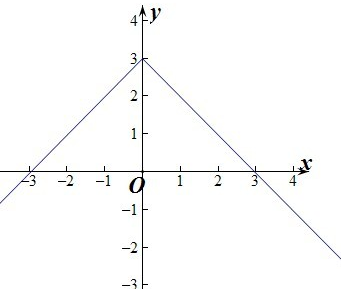：解：因为y=f（x）为偶函数，所以
f(x)+f(-x)
2x
=
2f(x)
2x
=
f(x)
x
＜0，
所以不等式等价为
x＞0
f(x)＜0
或
x＜0
f(x)＞0
．
因为函数y=f（x）为偶函数，且在（0，+∞）上是减函数，又f（3）=0，
所以解得x＞3或-3＜x＜0，
即不等式的解集为（-3，0）∪（3，+∞）．
故选C．
点评：本题主要考查函数奇偶性的应用，利用数形结合的思想是解决本题的关键．
练习册系列答案
相关题目
已知数列{an}，{bn}与函数f（x），g（x），x∈R满足条件：an=bn，f（bn）=g（bn+1）（n∈N*）．
（I）若f（x）≥tx+1，t≠0，t≠2，g（x）=2x，f（b）≠g（b），
limn→∞
an存在，求x的取值范围；
（II）若函数y=f（x）为R上的增函数，g（x）=f-1（x），b=1，f（1）＜1，证明对任意n∈N*，an+1＜an（用t表示）．
给出以下命题，其中正确命题序号为
（1）（3）（5）
（1）（3）（5）

（1）若函数y=f（x）为偶函数，则函数y=f （x-1）的图象关于直线x=1 对称；
（2）“x≠1”是“x2≠1”的充分不必要条件；
（3）函数y=2lg(x2-2)既是偶函数，又在区间[2，8]上是增函数；
（4）已知f′（x）是函数y=f（x）的导函数，若f′（x0）=0，则x0必为函数的极值点；
（5）某城市现有人口a万人，预计年平均增长率为p．那么该城市第十年年初的人口总数为a（1+p）9万人．
已知函数f（x）=（x2+ax+3）ex（x，a∈R）
（1）当a=0时，求函数f（x）的图象在A（1，f（1））处的切线方程．
（2）若函数y=f（x）为单调函数，求实数a的取值范围．
（3）当a=-3时，求f（x）的极小值．
设函数y=f（x），x∈R．
（1）若函数y=f（x）为偶函数并且图象关于直线x=a（a≠0）对称，求证：函数y=f（x）为周期函数．
（2）若函数y=f（x）为奇函数并且图象关于直线x=a（a≠0）对称，求证：函数y=f（x）是以4a为周期的函数．
（3）请对（2）中求证的命题进行推广，写出一个真命题，并予以证明．
已知函数f（x）=x2-4-k|x-2|．
（1）若函数y=f（x）为偶函数，求k的值；
（2）求函数y=f（x）在区间[0，4]上的最大值；
（3）若函数y=f（x）有且仅有一个零点，求实数k的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网