题目内容
下列命题正确的是 (只须填写命题的序号即可)(1)函数
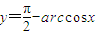 是奇函数;
是奇函数;(2)在△ABC中,A+B<
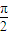 是sinA<cosB的充要条件;
是sinA<cosB的充要条件;(3)当α∈(0,π)时,cosα+sinα=m(0<m<1),则α一定是钝角,且|tanα|>1;
(4)要得到函数y=cos(
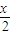 -
- )的图象,只需将y=sin
)的图象,只需将y=sin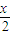 的图象向左平移
的图象向左平移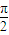 个单位.
个单位.
【答案】分析:对于(1)设f(x)= ,利用奇偶函数的定义结合反三角函数的性质即可判断函数
,利用奇偶函数的定义结合反三角函数的性质即可判断函数 是奇函数;(2)在△ABC中,A+B<
是奇函数;(2)在△ABC中,A+B< ⇒A<
⇒A< -B⇒sinA<sin(
-B⇒sinA<sin( -B)⇒sinA<cosB,反之不成立;(3)当α∈(0,π)时,cosα+sinα=m平方得到cosα<0,则α一定是钝角;(4)将y=sin
-B)⇒sinA<cosB,反之不成立;(3)当α∈(0,π)时,cosα+sinα=m平方得到cosα<0,则α一定是钝角;(4)将y=sin 的图象向左平移
的图象向左平移 个单位得到函数y=cos[
个单位得到函数y=cos[ (x+
(x+ )-
)- ]即得到函数y=cos(
]即得到函数y=cos( +
+ )的图象,故错.
)的图象,故错.
解答:解:对于(1)设f(x)= ,则f(-x)=
,则f(-x)= =
= =-f(x),故函数
=-f(x),故函数 是奇函数;正确.
是奇函数;正确.
(2)在△ABC中,A+B< ⇒A<
⇒A< -B⇒sinA<sin(
-B⇒sinA<sin( -B)⇒sinA<cosB,反之不成立;故(2)错.
-B)⇒sinA<cosB,反之不成立;故(2)错.
(3)当α∈(0,π)时,cosα+sinα=m平方得:
cos2α+sin2α+2cosαsinα=m2,⇒2cosαsinα=m2-1<0,⇒cosα<0,
则α一定是钝角,且|tanα|>1;故(3)正确;
(4)将y=sin 的图象向左平移
的图象向左平移 个单位得到函数y=cos[
个单位得到函数y=cos[ (x+
(x+ )-
)- ]即得到函数y=cos(
]即得到函数y=cos( +
+ )的图象,得不到函数y=cos(
)的图象,得不到函数y=cos( -
- )的图象,故错.
)的图象,故错.
故答案为:(1),(3).
点评:本小题主要考查函数单调性的应用、函数y=Asin(ωx+φ)的图象变换、必要条件、充分条件与充要条件的判断等基础知识,考查运算求解能力、化归与转化思想.属于基础题.
 ,利用奇偶函数的定义结合反三角函数的性质即可判断函数
,利用奇偶函数的定义结合反三角函数的性质即可判断函数 是奇函数;(2)在△ABC中,A+B<
是奇函数;(2)在△ABC中,A+B< ⇒A<
⇒A< -B⇒sinA<sin(
-B⇒sinA<sin( -B)⇒sinA<cosB,反之不成立;(3)当α∈(0,π)时,cosα+sinα=m平方得到cosα<0,则α一定是钝角;(4)将y=sin
-B)⇒sinA<cosB,反之不成立;(3)当α∈(0,π)时,cosα+sinα=m平方得到cosα<0,则α一定是钝角;(4)将y=sin 的图象向左平移
的图象向左平移 个单位得到函数y=cos[
个单位得到函数y=cos[ (x+
(x+ )-
)- ]即得到函数y=cos(
]即得到函数y=cos( +
+ )的图象,故错.
)的图象,故错.解答:解:对于(1)设f(x)=
 ,则f(-x)=
,则f(-x)= =
= =-f(x),故函数
=-f(x),故函数 是奇函数;正确.
是奇函数;正确.(2)在△ABC中,A+B<
 ⇒A<
⇒A< -B⇒sinA<sin(
-B⇒sinA<sin( -B)⇒sinA<cosB,反之不成立;故(2)错.
-B)⇒sinA<cosB,反之不成立;故(2)错.(3)当α∈(0,π)时,cosα+sinα=m平方得:
cos2α+sin2α+2cosαsinα=m2,⇒2cosαsinα=m2-1<0,⇒cosα<0,
则α一定是钝角,且|tanα|>1;故(3)正确;
(4)将y=sin
 的图象向左平移
的图象向左平移 个单位得到函数y=cos[
个单位得到函数y=cos[ (x+
(x+ )-
)- ]即得到函数y=cos(
]即得到函数y=cos( +
+ )的图象,得不到函数y=cos(
)的图象,得不到函数y=cos( -
- )的图象,故错.
)的图象,故错.故答案为:(1),(3).
点评:本小题主要考查函数单调性的应用、函数y=Asin(ωx+φ)的图象变换、必要条件、充分条件与充要条件的判断等基础知识,考查运算求解能力、化归与转化思想.属于基础题.

练习册系列答案
相关题目