题目内容
【题目】如图,在四棱锥![]() 中,
中,![]() 丄平面
丄平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)证明![]() 丄
丄![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)设![]() 为棱
为棱![]() 上的点,满足异面直线
上的点,满足异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,求
,求![]() 的长.
的长.
【答案】(1)见证明;(2) ![]() ;(3)
;(3) ![]()
【解析】
(1)要证异面直线垂直,即证线面垂直,本题需证![]() 平面
平面![]()
(2)作![]() 于点
于点![]() ,连接
,连接![]() 。
。 ![]() 为二面角
为二面角![]() 的平面角,在
的平面角,在![]() 中解出
中解出![]() 即可。
即可。
(3)过点![]() 作
作![]() 的平行线与线段
的平行线与线段![]() 相交,交点为
相交,交点为![]() ,连接
,连接![]() ,
,![]() ;计算出AF、BF,再在
;计算出AF、BF,再在![]() 中利用
中利用![]() 的余弦公式,解出EF,即可求出AE的长
的余弦公式,解出EF,即可求出AE的长
(1)证明:由![]() 平面
平面![]() ,可得
,可得![]() ,
,
又由![]() ,
,![]() ,故
,故![]() 平面
平面![]() 。
。
又![]() 平面
平面![]() ,所以
,所以![]() 。
。
(2)如图,作![]() 于点
于点![]() ,连接
,连接![]() 。
。
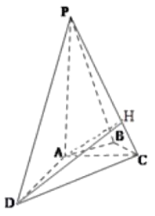
由![]() ,
,![]() ,可得
,可得![]() 平面
平面![]() 。
。
因此![]() ,从而
,从而![]() 为二面角
为二面角![]() 的平面角。
的平面角。
在![]() 中,
中,![]() ,
,![]() ,由此得
,由此得![]()
由(1)知![]() ,故在
,故在![]() 中,
中,![]()
因此![]() 所以二面角
所以二面角
![]() 的正弦值为
的正弦值为![]() 。
。
(3)因为![]() ,故过点
,故过点![]() 作
作![]() 的平行线必与线段
的平行线必与线段![]() 相交,
相交,
设交点为![]() ,连接
,连接![]() ,
,![]() ;
;
∴![]() 或其补角为异面直线
或其补角为异面直线![]() 与
与![]() 所成的角;
所成的角;
由于![]() ,故
,故![]() ;
;
在![]() 中,
中,![]() ,
,![]() ;
;
∴![]() ;
;
∴在![]() 中,由
中,由![]() ,
,![]() ,
,![]()
可得:![]() ;
;
由余弦定理,![]() 可得,
可得,![]() ,
,
解得:![]() ,设
,设![]() ;
;
在![]() 中,
中,![]() ;
;
在![]() 中,
中,![]() ;
;
∴在![]() 中,
中,![]() ,∴
,∴![]() ;
;
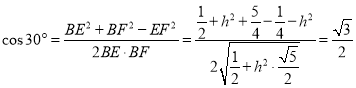 ;
;
解得![]() ;∴
;∴![]() 。
。

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
【题目】某个产品有若千零部件构成,加工时需要经过6道工序,分别记为![]() .其中,有些工序因为是制造不同的零部件,所以可以在几台机器上同时加工;有些工序因为是对同一个零部件进行处理,所以存在加工顺序关系.若加工工序
.其中,有些工序因为是制造不同的零部件,所以可以在几台机器上同时加工;有些工序因为是对同一个零部件进行处理,所以存在加工顺序关系.若加工工序![]() 必须要在工序
必须要在工序![]() 完成后才能开工,则称
完成后才能开工,则称![]() 为
为![]() 的紧前工序.现将各工序的加工次序及所需时间(单位:小时)列表如下:
的紧前工序.现将各工序的加工次序及所需时间(单位:小时)列表如下:
工序 |
|
|
|
|
|
|
加工时间 | 3 | 4 | 2 | 2 | 2 | 1 |
紧前工序 | 无 |
| 无 |
|
|
|
现有两台性能相同的生产机器同时加工该产品,则完成该产品的最短加工时间是__________小时.(假定每道工序只能安排在一台机器上,且不能间断).




