题目内容
（1）已知点A（a，6）到直线3x-4y=2的距离d=4，求a的值．（2）在直线x+3y=0求一点P，使它到原点的距离与到直线x+3y-2=0的距离相等．
分析：（1）把点A（a，6）直接代入点到直线的距离公式得到一个方程，解方程求得a的值．
（2）设点P的坐标为（-3t，t），则由题意得
=
，解之可得t值．
（2）设点P的坐标为（-3t，t），则由题意得
| (-3t)2+t2 |
| |-3t+3t-2| | ||
|
解答：解：（1）由点到直线的距离公式得 d=
=4，解得a=2，或a=
．
（2）设点P的坐标为（-3t，t），则
=
，解之得t=±
．
∴点P的坐标为(
，-
)或(-
，
)．
| |3a-4×6-2| | ||
|
| 46 |
| 3 |
（2）设点P的坐标为（-3t，t），则
| (-3t)2+t2 |
| |-3t+3t-2| | ||
|
| 1 |
| 5 |
∴点P的坐标为(
| 3 |
| 5 |
| 1 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
点评：本题考查点到直线的距离公式的应用，以及两点间的距离公式的应用．
练习册系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
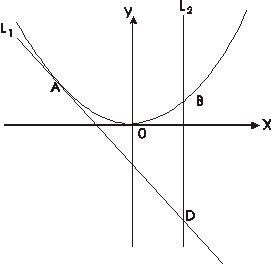已知点A（-1，2）是抛物线C：y=2x2上的点，直线l1过点A，且与抛物线C相切，直线l2：x=a（a≠-1）交抛物线C于点B，交直线l1于点D．