题目内容
已知三棱锥S—ABC中，相对棱SB与AC所成角为θ，SB=a，AC=b，SB、AC间的距离为d,求此三棱锥的体积.
解析：如图，作BD
AC，连结CD、SD，则∠SBD=θ或∠SBD=π-θ，AC∥平面SBD，
故SB、AC间的距离等于点C到平面SBD的距离d，
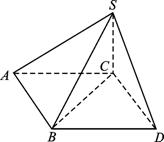
即三棱锥C—SBD的高为d.
∴VS-ABC=VS-BCD=VC-SBD=
S△SBD·d=
·
·SB·BD·sin∠SBD·d=
abdsinθ.
练习册系列答案
轻松暑假总复习系列答案
相关题目