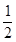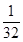题目内容
(本小题满分14分)
已知函数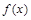 在
在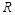 上有定义,对任意实数
上有定义,对任意实数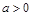 和任意实数
和任意实数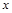 ,都有
,都有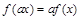 .
.
(Ⅰ)证明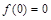 ;
;
(Ⅱ)证明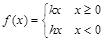 (其中k和h均为常数);
(其中k和h均为常数);
(Ⅲ)当(Ⅱ)中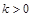 的时,设
的时,设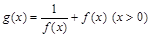 ,讨论
,讨论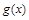 在
在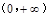 内的单调性.
内的单调性.
已知函数
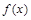 在
在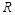 上有定义,对任意实数
上有定义,对任意实数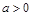 和任意实数
和任意实数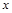 ,都有
,都有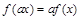 .
. (Ⅰ)证明
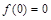 ;
;(Ⅱ)证明
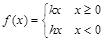 (其中k和h均为常数);
(其中k和h均为常数);(Ⅲ)当(Ⅱ)中
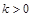 的时,设
的时,设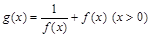 ,讨论
,讨论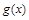 在
在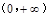 内的单调性.
内的单调性.(Ⅰ)证明:见解析;(Ⅱ)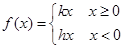
(Ⅲ)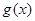 在区间
在区间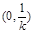 内单调递减, 在区间(
内单调递减, 在区间(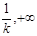 )内单调递增.
)内单调递增.
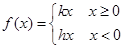
(Ⅲ)
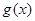 在区间
在区间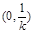 内单调递减, 在区间(
内单调递减, 在区间(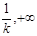 )内单调递增.
)内单调递增.本小题主要考查函数的概念、导数应用、函数的单调区间和极值等知识,考查运用数学知识解决问题及推理的能力。
(1)对于任意的a>0,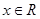 ,均有
,均有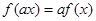 ①在①中取
①在①中取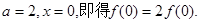
(2) 令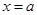 时,∵
时,∵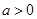 ,∴
,∴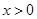 ,则
,则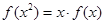
而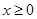 时,
时,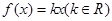 ,则
,则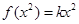
而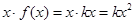 , ∴
, ∴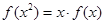 ,即
,即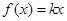 成立
成立
赋值法得到结论。
(3)由(Ⅱ)中的③知,当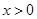 时,
时,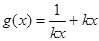 ,
,
分析导数得到单调区间。
(Ⅰ)证明:对于任意的a>0,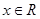 ,均有
,均有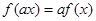 ①
①
在①中取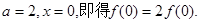
∴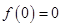 ②
②
(Ⅱ)证法一:当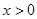 时,由①得
时,由①得 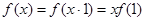
取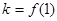 ,则有
,则有 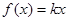 ③
③
当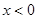 时,由①得
时,由①得 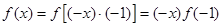
取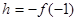 ,则有
,则有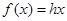 ④
④
综合②、③、④得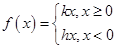 ;
;
证法二:
令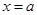 时,∵
时,∵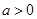 ,∴
,∴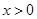 ,则
,则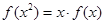
而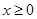 时,
时,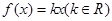 ,则
,则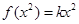
而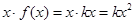 , ∴
, ∴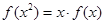 ,即
,即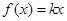 成立
成立
令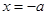 ,∵
,∵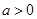 ,∴
,∴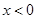 ,则
,则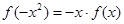
而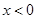 时,
时,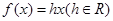 ,则
,则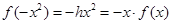
即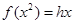 成立。综上知
成立。综上知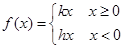
(Ⅲ)解法1:由(Ⅱ)中的③知,当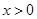 时,
时,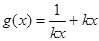 ,
,
从而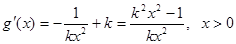
又因为k>0,由此可得
所以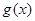 在区间
在区间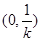 内单调递减,在区间(
内单调递减,在区间(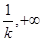 )内单调递增。
)内单调递增。
解法2:由(Ⅱ)中的③知,当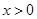 时,
时,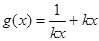 ,
,
设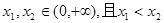 则
则
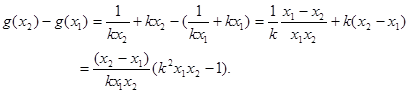
又因为k>0,所以
(i)当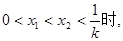
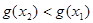 ;
;
(ii)当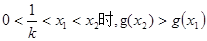
所以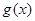 在区间
在区间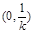 内单调递减, 在区间(
内单调递减, 在区间(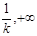 )内单调递增.
)内单调递增.
(1)对于任意的a>0,
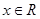 ,均有
,均有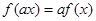 ①在①中取
①在①中取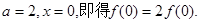
(2) 令
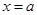 时,∵
时,∵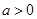 ,∴
,∴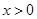 ,则
,则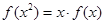
而
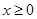 时,
时,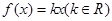 ,则
,则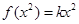
而
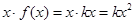 , ∴
, ∴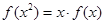 ,即
,即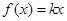 成立
成立赋值法得到结论。
(3)由(Ⅱ)中的③知,当
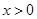 时,
时,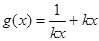 ,
,分析导数得到单调区间。
(Ⅰ)证明:对于任意的a>0,
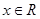 ,均有
,均有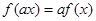 ①
①在①中取
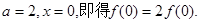
∴
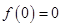 ②
②(Ⅱ)证法一:当
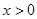 时,由①得
时,由①得 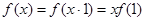
取
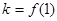 ,则有
,则有 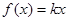 ③
③当
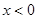 时,由①得
时,由①得 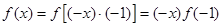
取
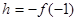 ,则有
,则有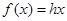 ④
④综合②、③、④得
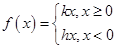 ;
;证法二:
令
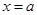 时,∵
时,∵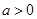 ,∴
,∴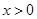 ,则
,则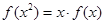
而
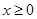 时,
时,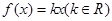 ,则
,则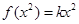
而
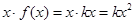 , ∴
, ∴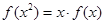 ,即
,即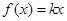 成立
成立令
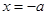 ,∵
,∵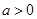 ,∴
,∴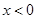 ,则
,则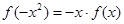
而
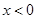 时,
时,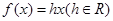 ,则
,则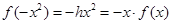
即
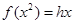 成立。综上知
成立。综上知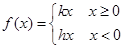
(Ⅲ)解法1:由(Ⅱ)中的③知,当
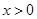 时,
时,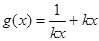 ,
,从而
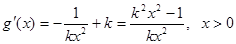
又因为k>0,由此可得
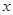 | 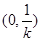 | 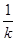 | 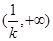 |
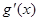 | - | 0 | + |
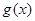 | ↘ | 极小值2 | ↗ |
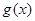 在区间
在区间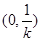 内单调递减,在区间(
内单调递减,在区间(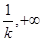 )内单调递增。
)内单调递增。解法2:由(Ⅱ)中的③知,当
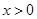 时,
时,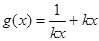 ,
,设
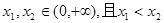 则
则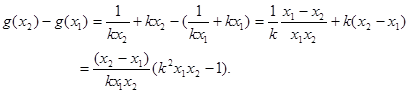
又因为k>0,所以
(i)当
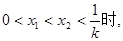
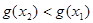 ;
;(ii)当
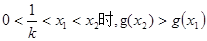
所以
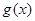 在区间
在区间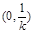 内单调递减, 在区间(
内单调递减, 在区间(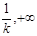 )内单调递增.
)内单调递增.
练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 则
则 的值为( )
的值为( ) ,则f(3)的值为 .
,则f(3)的值为 .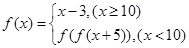 ,则
,则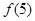 =( )
=( ) ,则
,则 = .
= .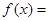
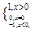 ,
, 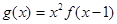 ,则函数
,则函数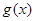 的递减区间是( )
的递减区间是( )



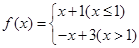 ,那么
,那么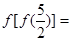
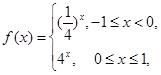 则
则 = ( )
= ( )



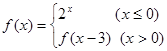 ,则
,则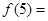 ( )
( )