题目内容
将边长为1的正方形ABCD,沿对角线AC折起,使BD=![]() .则三棱锥D-ABC的体积为
.则三棱锥D-ABC的体积为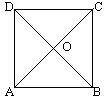
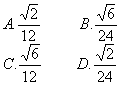
B
解析:
设AC、BD交于O点,则BO⊥AC
且DO⊥AC,在折起后,这个垂直关系不变,因此∠BOD是二面角B-AC-D的平面角.
由于△DOB中三边长已知,所以可求出∠BOD:


这是问题的一方面,另一方面为了求体积,应求出高,这个高实际上是△DOB中,OB边上的高DE,理由是:

∵DE⊥OB
∴DE⊥面ABC. 
由cos∠DOB=![]() ,知sin∠DOE=
,知sin∠DOE=![]()
∴DE=![]()
∴![]()
应选(B)

练习册系列答案
相关题目
将边长为1的正方形ABCD沿对角线BD折起,使得点A到点A′的位置,且A′C=1,则折起后二面角A′-DC-B的大小( )
A、arctan
| ||||
B、
| ||||
C、arctan
| ||||
D、
|
 将边长为1的正方形ABCD沿对角线BD折成直二面角,若点P满足
将边长为1的正方形ABCD沿对角线BD折成直二面角,若点P满足| BP |
| 1 |
| 2 |
| BA |
| 1 |
| 2 |
| BC |
| BD |
| BP |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|