题目内容
设f(x)=a
-lnx(a>0):
(1)若f(x)在[1,+∞)上递增,求a的取值范围;
(2)求f(x)在[1,4]上的最小值.
| x |
(1)若f(x)在[1,+∞)上递增,求a的取值范围;
(2)求f(x)在[1,4]上的最小值.
(1)求导函数,可得f′(x)=
∵f(x)在[1,+∞)上递增,
∴在[1,+∞)上,f′(x)=
≥0恒成立
∴在[1,+∞)上,a≥
∴a≥2
∴a的取值范围为[2,+∞);
(2)由f′(x)=
,x∈[1,4]
①当a≥2时,在x∈[1,4]上,f'(x)≥0,∴fmin(x)=f(1)=a(8分)
②当0≤a≤1时,在x∈[1,4]上,f'(x)≤0,∴fmin(x)=f(4)=2a-2ln2(10分)
③当1<a<2时,在x∈[1,
]上f'(x)≤0,在x∈[
,4]上f'(x)≥0
此时fmin(x)=f(
)=2-2ln2+2lna
综上所述:fmin(x)=
(13分)
a
| ||
| 2x |
∵f(x)在[1,+∞)上递增,
∴在[1,+∞)上,f′(x)=
a
| ||
| 2x |
∴在[1,+∞)上,a≥
| 2 | ||
|
∴a≥2
∴a的取值范围为[2,+∞);
(2)由f′(x)=
a
| ||
| 2x |
①当a≥2时,在x∈[1,4]上,f'(x)≥0,∴fmin(x)=f(1)=a(8分)
②当0≤a≤1时,在x∈[1,4]上,f'(x)≤0,∴fmin(x)=f(4)=2a-2ln2(10分)
③当1<a<2时,在x∈[1,
| 4 |
| a2 |
| 4 |
| a2 |
此时fmin(x)=f(
| 4 |
| a2 |
综上所述:fmin(x)=
|

练习册系列答案
相关题目
 R),
R), =
2x2+3x-1,h (x)为f
(x)、g(x)在R上生成的一个二次函数.
=
2x2+3x-1,h (x)为f
(x)、g(x)在R上生成的一个二次函数. ,若h (x)为偶函数,求
,若h (x)为偶函数,求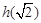 ;
; ,若h (x)同时也是g(x)、l(x) 在R上生成的一个函数,求a+b的最小值;
,若h (x)同时也是g(x)、l(x) 在R上生成的一个函数,求a+b的最小值;