题目内容

ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证:AP∥GH.

证明:如图,连结AC交BD于O,连结MO,

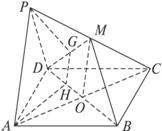
∵四边形ABCD是平行四边形,

∴O是AC的中点.又M是PC的中点,

∴AP∥OM.

根据直线和平面平行的判定定理,

则有PA∥平面BMD.

∵平面PAHG∩平面BMD=GH,

根据直线和平面平行的性质定理,

∴PA∥GH.


练习册系列答案
相关题目
例2．已知ABCD是平行四边形，求证：|
AC
|2+|
BD
|2=2(|
AB
|2+|
AD
|2).
如图，在四棱锥S-ABCD中，SD⊥底面ABCD，底面ABCD是平行四边形，∠BAD=30°，AB=2，AD=
3
，E是SC的中点．
（Ⅰ）求证：SA∥平面BDE；
（Ⅱ）求证：AD⊥SB；
（Ⅲ）若SD=2，求棱锥C-BDE的体积．
在如图所示的几何体中，四边形ABCD是平行四边形，∠ABD=90°，EB⊥平面ABCD，EF∥AB ，  AB=2 ，  EB=
3
 ，  EF=1 ，BC=
13

且M是BD的中点．
（1）求证：EM∥平面ADF；
（2）求直线DF和平面ABCD所成角的正切值；
（3）求二面角D-AF-B的大小．
如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，PA⊥平面ABCD，点M、N分别为BC、PA的中点，且PA=AD=2，AB=1，AC=
3
．
（Ⅰ）证明：CD⊥平面PAC；
（Ⅱ）在线段PD上是否存在一点E，使得NM∥平面ACE；若存在，求出PE的长；若不存在，说明理由．
如图，已知四棱锥V-ABCD，底面ABCD是平行四边形，点V在平面ABCD上的射影E在AD边上，且AE=
1
3
ED，VE=4，BE=EC=2，∠BEC=90°．
（Ⅰ）设F是BC的中点，求异面直线EF与VC所成角的余弦值；
（Ⅱ）设点P在棱VC上，且DP⊥EC．求
VP
PC
的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网