题目内容
已知函数f(x)=ln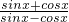 .
.
(1)判断f(x)的奇偶性;
(2)猜测f(x)的周期并证明;
(3)写出f(x)的单调递减区间.
解:(1)由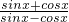 =
=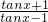 >0,可得 tanx<-1 或tanx>1,cosx=0.
>0,可得 tanx<-1 或tanx>1,cosx=0.
∴x>kπ+ ,或x<kπ-
,或x<kπ- ,或 x=2kπ±
,或 x=2kπ± ,k∈z,
,k∈z,
故函数的定义域为(kπ+ ,kπ+
,kπ+ )∪( kπ-
)∪( kπ- ,kπ-
,kπ- ),或x=2kπ±
),或x=2kπ± ,k∈z,故定义域关于原点对称.
,k∈z,故定义域关于原点对称.
∵f( x)=ln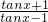 ,∴f(-x)=ln
,∴f(-x)=ln 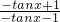 =ln
=ln 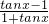 =-ln
=-ln 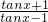 =-f( x),
=-f( x),
故函数f( x)为奇函数.
(2)由于tanx的周期等于π,故f(x)的周期等于π,证明如下:
∵f(π+x)=ln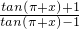 =ln
=ln 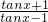 =f( x),故函数f( x)的周期等于π.
=f( x),故函数f( x)的周期等于π.
(3)f(x)的单调递减区间即函数t=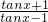 =1+
=1+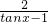 的减区间,即tanx<-1 或tanx>1 时的增区间,
的减区间,即tanx<-1 或tanx>1 时的增区间,
故f(x)的单调递减区间为(kπ+ ,kπ+
,kπ+ ),( kπ-
),( kπ- ,kπ-
,kπ- ).
).
分析:(1)求出函数f( x) 的定义域关于原点对称,再由f(-x)=-f( x),可得函数f( x)为奇函数.
(2)由于tanx的周期等于π,故f(x)的周期等于π,证明根据f(π+x)=f( x).
(3)f(x)的单调递减区间即函数t=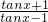 =1+
=1+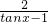 的减区间,即tanx<-1 或tanx>1 时的增区间,由此求得f(x)的单调递减区间.
的减区间,即tanx<-1 或tanx>1 时的增区间,由此求得f(x)的单调递减区间.
点评:本题考查三角函数的周期性、奇偶性和单调性,化简函数f( x) 的解析式为 ln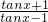 ,是解题的关键.
,是解题的关键.
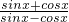 =
=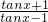 >0,可得 tanx<-1 或tanx>1,cosx=0.
>0,可得 tanx<-1 或tanx>1,cosx=0.∴x>kπ+
 ,或x<kπ-
,或x<kπ- ,或 x=2kπ±
,或 x=2kπ± ,k∈z,
,k∈z,故函数的定义域为(kπ+
 ,kπ+
,kπ+ )∪( kπ-
)∪( kπ- ,kπ-
,kπ- ),或x=2kπ±
),或x=2kπ± ,k∈z,故定义域关于原点对称.
,k∈z,故定义域关于原点对称.∵f( x)=ln
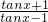 ,∴f(-x)=ln
,∴f(-x)=ln 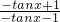 =ln
=ln 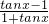 =-ln
=-ln 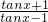 =-f( x),
=-f( x),故函数f( x)为奇函数.
(2)由于tanx的周期等于π,故f(x)的周期等于π,证明如下:
∵f(π+x)=ln
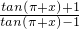 =ln
=ln 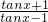 =f( x),故函数f( x)的周期等于π.
=f( x),故函数f( x)的周期等于π.(3)f(x)的单调递减区间即函数t=
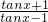 =1+
=1+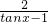 的减区间,即tanx<-1 或tanx>1 时的增区间,
的减区间,即tanx<-1 或tanx>1 时的增区间,故f(x)的单调递减区间为(kπ+
 ,kπ+
,kπ+ ),( kπ-
),( kπ- ,kπ-
,kπ- ).
).分析:(1)求出函数f( x) 的定义域关于原点对称,再由f(-x)=-f( x),可得函数f( x)为奇函数.
(2)由于tanx的周期等于π,故f(x)的周期等于π,证明根据f(π+x)=f( x).
(3)f(x)的单调递减区间即函数t=
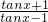 =1+
=1+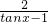 的减区间,即tanx<-1 或tanx>1 时的增区间,由此求得f(x)的单调递减区间.
的减区间,即tanx<-1 或tanx>1 时的增区间,由此求得f(x)的单调递减区间.点评:本题考查三角函数的周期性、奇偶性和单调性,化简函数f( x) 的解析式为 ln
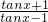 ,是解题的关键.
,是解题的关键. 
练习册系列答案
相关题目