Question

（2014•信阳一模）已知函数f（x）=Asin（ωx+φ），（x∈R，A＞0，ω＞0，|φ|＜

π

2

）的部分图象如图所示：
（1）试确定f（x）的解析式；
（2）若f（

α

2π

）=

1

3

，求cos(

2π

3

-α)的值．

Answer 1

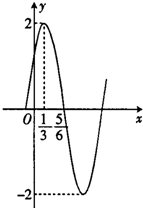
分析：（1）由图可知，A=2，

T

4

=

1

2

，可求得ω，再利用

1

3

ω+φ=

π

2

可求得φ，从而可求得f（x）的解析式；
（2）由（1）知f（x）的解析式，结合已知f（

α

2π

）=

1

3

，可求得α的三角函数知，最后利用两角差的余弦计算即可求cos（

2π

3

-α）的值．

解答：解：（1）由图可知，A=2，

T

4

=

5

6

-

1

3

=

1

2

，又ω＞0，
∴T=

2π

ω

=2，
∴ω=π；
由图可知，f（x）=Asin（ωx+φ）经过（

1

3

，2），
∴

1

3

ω+φ=

π

2

，即

π

3

+φ=

π

2

，
∴φ=

π

6

，
∴f（x）=2sin（πx+

π

6

）；
（2）∵f（

α

2π

）=

1

3

，
∴2sin（

α

2

+

π

6

）=

1

3

，
∴sin（

α

2

+

π

6

）=cos[

π

2

-（

α

2

+

π

6

）]=cos（

π

3

-

α

2

）=

1

6

，
∴cos（

2π

3

-α）=2cos2(

π

3

-

α

2

)-1=2×

1

36

-1=-

17

18

．

点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，考查三角函数中的恒等变换应用，考查两角差的余弦，属于中档题．