题目内容
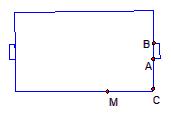
设足球场宽65米，球门宽7米，当足球运动员沿边路带球突破，距底线多远处射门，对球门所张的角最大？（保留两位小数）分析：先设∠AMB=α，∠AMC=β，MC=x得到 tanβ=
，tan(α+β)=
，再结合两角差的正切公式求出tanα，最后结合基本不等式即可求出结论．
| 29 |
| x |
| 36 |
| x |
解答：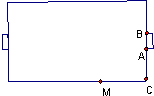
解：如图
设∠AMB=α，∠AMC=β，MC=x
则 tanβ=
，tan(α+β)=
，
tanα=tan[(α+β)-β]=
=
=
=
≤
当且仅当x=
，即x=6
≈32.31时，tanα最大，
因为α是锐角，所以此时α最大，即对球门的张角最大．
解：如图设∠AMB=α，∠AMC=β，MC=x
则 tanβ=
| 29 |
| x |
| 36 |
| x |
tanα=tan[(α+β)-β]=
| tan(α+β)-tanβ |
| 1+tan(α+β)tanβ |
=
| ||||
1+
|
| 7x |
| x2+36×29 |
| 7 | ||
x+
|
| 7 | ||
12
|
当且仅当x=
| 36×29 |
| x |
| 29 |
因为α是锐角，所以此时α最大，即对球门的张角最大．
点评：本题主要考查三角知识在解三角形中的实际应用．解决这类问题的关键在于对公式的熟练掌握以及灵活运用．
练习册系列答案
名校课堂系列答案
相关题目
