题目内容
已知函数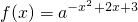
，（a＞0，a≠1）
（1）当a=3时，求f（x）的定义域和值域
（2）求f（x）的单调区间．
解：（1）当a=3时，对任意x∈R时，函数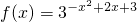
均有意义，故函数的定义域为（-∞，+∞），
而由而二次函数的知识可得-x2+2x+3=-（x-1）2+4≤4，故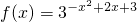≤34=81，
而由指数函数的值域可知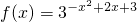＞0，故函数的值域为（0，81]
（2）由二次函数的知识可知函数t=-x2+2x+3的单调递增区间为（-∞，1]，单调递减区间为[1，+∞）．
由复合函数的单调性可知：当a＞1时，函数单调增区间为（-∞，1]函数减区间为[1，+∞）；
当0＜a＜1时，函数单调减区间为（-∞，1]；函数增区间为[1，+∞）．
分析：（1）把a=3代入可得函数解析式，易得定义域，由二次函数的值域可得f（x）的值域；
（2）先得函数t=-x2+2x+3的单调区间，再由复合函数的单调性可得答案．
点评：本题考查函数的单调性的判断与证明，涉及函数的值域的求解和分类讨论的思想，属基础题．
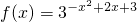均有意义，故函数的定义域为（-∞，+∞），而由而二次函数的知识可得-x2+2x+3=-（x-1）2+4≤4，故
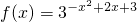≤34=81，而由指数函数的值域可知
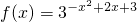＞0，故函数的值域为（0，81]（2）由二次函数的知识可知函数t=-x2+2x+3的单调递增区间为（-∞，1]，单调递减区间为[1，+∞）．
由复合函数的单调性可知：当a＞1时，函数单调增区间为（-∞，1]函数减区间为[1，+∞）；
当0＜a＜1时，函数单调减区间为（-∞，1]；函数增区间为[1，+∞）．
分析：（1）把a=3代入可得函数解析式，易得定义域，由二次函数的值域可得f（x）的值域；
（2）先得函数t=-x2+2x+3的单调区间，再由复合函数的单调性可得答案．
点评：本题考查函数的单调性的判断与证明，涉及函数的值域的求解和分类讨论的思想，属基础题．
练习册系列答案
相关题目
，其中a＞0且a≠1．
，其中a＞0．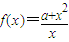
，（a＞0），x∈（0，b），则下列判断正确的是（ ）
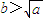时，f（x）的最小值为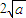
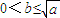时，f（x）的最小值为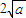
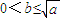时，f（x）的最小值为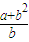
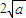
+bx（a＞0）且f′（1）=0，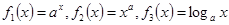
（其中a＞0，且a≠），在同一坐标系中画出其中两个函数在第一象限内的图像，其中正确的是