题目内容
已知向量 =(3,-4),
=(3,-4), =(6,-3),
=(6,-3), =(5-m,-3-m).
=(5-m,-3-m).
(1)若点A,B,C不能构成三角形,求实数m满足的条件;
(2)若△ABC为直角三角形,求实数m的值.
解:(1)∵ =(3,-4),
=(3,-4), =(6,-3),
=(6,-3), =(5-m,-3-m),
=(5-m,-3-m),
若A,B,C三点不能构成三角形,则这三点共线,
∵ =(3,1),
=(3,1), =(2-m,1-m),∴3(1-m)=2-m,
=(2-m,1-m),∴3(1-m)=2-m,
∴m= 即为满足的条件.
即为满足的条件.
(2)由题意,△ABC为直角三角形,
①若∠A=90°,则 ,∴3(2-m)+(1-m)=0,∴m=
,∴3(2-m)+(1-m)=0,∴m= .
.
②若∠B=90°,则 ,∵
,∵ (-1-m,-m),
(-1-m,-m),
∴3(-1-m)+(-m)=0,∴m=- .
.
③若∠C=90°,则 ,
,
∴(2-m)(-1-m)+(1-m)(-m)=0,∴m= .
.
综上可得,m= 或-
或- 或
或 .
.

练习册系列答案
相关题目
 )
)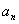 }的通项公式
}的通项公式 ,则
,则 等于( )
等于( ) ,则z的虚部为
,则z的虚部为  B、
B、 C、
C、 D、
D、
 展开式中
展开式中 的系数是
的系数是 B、
B、 C、
C、 D、
D、
 则
则
 C.
C.  D.
D.
 、
、 ,则线段
,则线段 的垂直平分线的方程是( )
的垂直平分线的方程是( ) B.
B. C.
C. D.
D.