题目内容
(本小题满分12分)
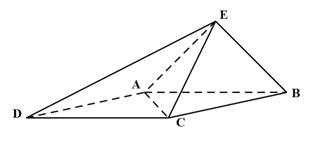
如图,已知四棱锥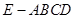 的底面为菱形,且
的底面为菱形,且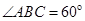 ,
,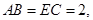
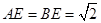 .
.
(I)求证:平面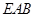
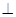 平面
平面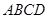 ;
;
(II)求二面角 的余弦值.
的余弦值.
【答案】
(I)证明:见解析
(II)二面角 的余弦值为
的余弦值为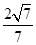
【解析】本试题主要考查了面面垂直和二面角的求解的综合运用。
(1)根据已知条件找到线面垂直,然后利用面面垂直的判定定理得到其证明。
(2)合理的建立空间直角坐标系,然后表示出点的坐标和向量的坐标,借助于平面的法向量,得到向量的夹角,从而得到二面角的平面角的大小。
(I)证明:取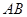 的中点
的中点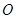 ,连接
,连接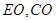
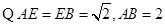
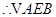 为等腰直角三角形
为等腰直角三角形
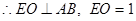 ……………………………………2分
……………………………………2分
又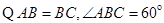
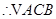 是等边三角形
是等边三角形
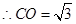 ,又
,又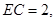
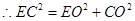 ,
,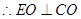 …………………………4分
…………………………4分
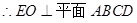 ,又
,又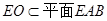
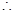 平面
平面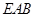
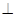 平面
平面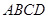 ;……………………………………6分
;……………………………………6分
(II)以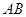 中点
中点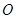 为坐标原点,以
为坐标原点,以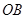 所在直线为
所在直线为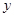 轴,
轴,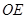 所在直线为
所在直线为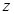 轴,建立空间直角坐标系如图所示,
轴,建立空间直角坐标系如图所示,
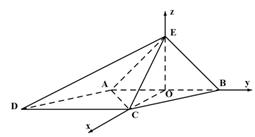
则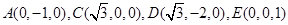
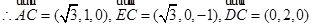 ……………………8分
……………………8分
设平面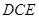 的法向量
的法向量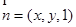
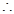
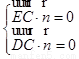 ,即
,即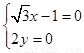 ,解得
,解得 ,
,
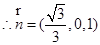
设平面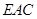 的法向量
的法向量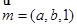
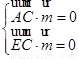 ,即
,即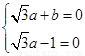 ,解得
,解得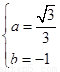 ,
,
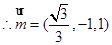 …………………………………………………………10分
…………………………………………………………10分
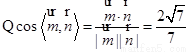
所以二面角 的余弦值为
的余弦值为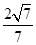 …………………………12分
…………………………12分

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目