题目内容
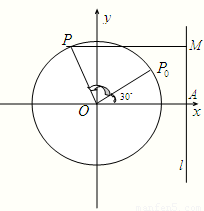
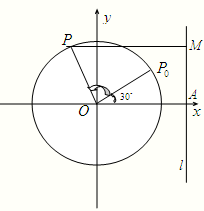 如图,圆O的半径为2,l为圆O外一条直线,圆心O到直线l的距离|OA|=3,P0为圆周上一点,且∠AOP0=
如图,圆O的半径为2,l为圆O外一条直线,圆心O到直线l的距离|OA|=3,P0为圆周上一点,且∠AOP0=| π | 6 |
①1秒钟后,点P的横坐标为
②t秒钟后,点P到直线l的距离用t可以表示为
分析:①1秒钟后,点P从P0处开始绕点O在圆周上按逆时针方向作匀速圆周运动,旋转了半周,此时点P与P0关于原点对称;②由题意,周期为2,则t秒钟后,旋转角为πt,故可求点P的横坐标,从而求出点P到直线l的距离.
解答:解:①1秒钟后,点P从P0处开始绕点O在圆周上按逆时针方向作匀速圆周运动,旋转了半周,此时点P与P0关于原点对称,从而点P的横坐标为-
;
②由题意,周期为2,则t秒钟后,旋转角为πt,则此时点P的横坐标为2cos(πt+
),所以点P到直线l的距离为3-2cos(πt+
),t≥0.
故答案为-
;3-2cos(πt+
),t≥0.
| 3 |
②由题意,周期为2,则t秒钟后,旋转角为πt,则此时点P的横坐标为2cos(πt+
| π |
| 6 |
| π |
| 6 |
故答案为-
| 3 |
| π |
| 6 |
点评:本题考查已知三角函数模型的应用问题,关键是搞清旋转角,理解三角函数的定义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
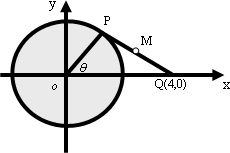
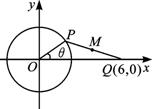
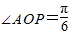 ,点P从P处开始以2秒一周的速度绕点O在圆周上按逆时针方向作匀速圆周运动.
,点P从P处开始以2秒一周的速度绕点O在圆周上按逆时针方向作匀速圆周运动.